Представление моделей систем в форме уравнений Ньютона и Лагранжа
Механические и электромеханические системы могут быть описаны на основе второго закона Ньютона. Для случая постоянной массы этот известный закон имеет вид:
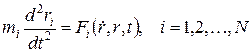 , (3.1)
, (3.1)
где 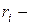 радиус-вектор
радиус-вектор 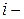 й материальной точки;
й материальной точки; 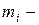 ее масса;
ее масса; 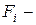 результирующая всех сил, приложенных к
результирующая всех сил, приложенных к 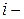 й точке (известные функции).
й точке (известные функции).
Уравнения (3.1) описываю поступательные движения материальной точки. Для вращательного движения существует форма второго закона Ньютона в виде:
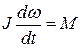 (3.2)
(3.2)
где 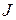 – момент инерции;
– момент инерции; 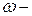 угловая скорость;
угловая скорость; 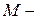 момент (сила, умноженная на плечо).
момент (сила, умноженная на плечо).
Оказывается, что движение тел подчиняется определенным соотношениям, связанным с энергией.
Рассмотрим случай одномерного (т.е. вдоль линии) движения тела с массой 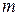 . Моделью такой системы является груз, соединенный пружиной со стенкой. Его кинетическая энергия равна
. Моделью такой системы является груз, соединенный пружиной со стенкой. Его кинетическая энергия равна
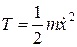 . (3.3)
. (3.3)
Потенциальная энергия движущегося тела, находящегося в поле действия силы пружины с коэффициентом жесткости «с», равна
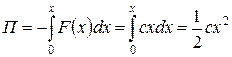 . (3.4)
. (3.4)
Закон сохранения полной энергии механической системы без потерь, находящейся в поле потенциальных сил, имеет вид:
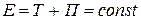 . (3.5)
. (3.5)
Дифференцируя (3.3) вначале по 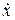 , а затем по
, а затем по 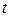 , получаем:
, получаем:
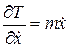 ,
, 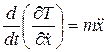 . (3.6)
. (3.6)
Равенство (3.4) продифференцируем по 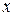 :
:
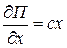 . (3.7)
. (3.7)
Применяя второй закон Ньютона к данному случаю, имеем
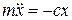 . (3.8)
. (3.8)
Приравнивая в соответствии с (3.8) левые части равенств (3.6) и (3.7), получаем:
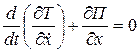 . (3.9)
. (3.9)
В общем случае уравнения движения Лагранжа второго рода для систем без потерь (консервативных) имеют вид:
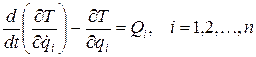 . (3.10)
. (3.10)
В аналитической механике переменные 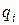 и
и 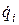 называют обобщенными координатами и скоростями, а присутствующие в правых частях обобщенные силы
называют обобщенными координатами и скоростями, а присутствующие в правых частях обобщенные силы 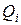 являются потенциальными (консервативными) и определяются выражениями:
являются потенциальными (консервативными) и определяются выражениями:
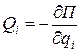 . (3.11)
. (3.11)
Разность между кинетической и потенциальной энергиями
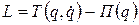 (3.12)
(3.12)
называют
лагранжианом (кинетическим потенциалом) системы. Из (3.10) с учетом определения (3.12) следует:
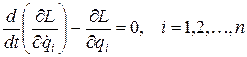 . (3.13)
. (3.13)
Заметим, что приведенная цепочка соотношений не является доказательством (3.13), которое на самом деле производится вариационным методом при решении задачи минимизации функционала действия
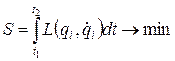 .
.
Уравнение (3.13) называют уравнением Эйлера-Лагранжа (или уравнением Лагранжа второго рода. Техника же получения уравнений движения на основе (3.13) примерно такая же, как при получении (3.9). При этом для каждой конкретной задачи необходимо знать зависимости кинетической и потенциальной энергии от обобщенных координат.
Пример. Рассмотрим математический маятник, представляющим собой груз массы 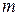 на конце невесомого абсолютно жесткого стержня длиной
на конце невесомого абсолютно жесткого стержня длиной 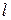 .
.
Кинетическая энергия системы, выраженная через линейную скорость 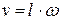 , определяется выражением:
, определяется выражением:
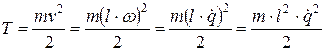 .
.
Потенциальная энергия системы, принимая во внимание, что при отклонении маятника на угол 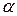 от вертикали он поднимается на высоту
от вертикали он поднимается на высоту 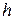 , равна:
, равна:
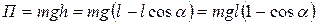 .
.
Переобозначив 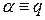 , получаем:
, получаем:
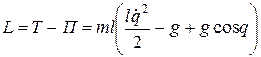 .
.
Далее:
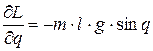 ;
; 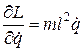 ;
; 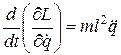 .
.
В итоге получается следующее уравнение в исходных обозначениях:
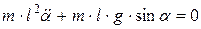 .
.
Дата добавления: 2016-04-02; просмотров: 801;
