Первая теорема подобия
Первая теорема (прямая теорема) подобия. Для того, чтобы системы
 и
и 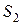 ,уравнения связи которых отвечают условию (2.4), были подобны, необходимо и достаточно, чтобы константы подобия удовлетворяли соотношениям
,уравнения связи которых отвечают условию (2.4), были подобны, необходимо и достаточно, чтобы константы подобия удовлетворяли соотношениям
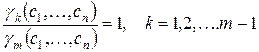 . (2.5)
. (2.5)
Доказательство.
Разделим (2.2) на 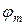 , а (2.3) на
, а (2.3) на 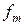 :
:
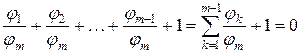 , (2.6)
, (2.6)
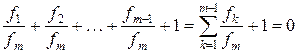 . (2.7)
. (2.7)
Используя условие (2.4), преобразуем (2.7):
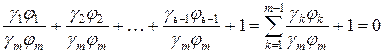 .
.
Из последнего выражения, с учетом (2.5), получаем (2.6). Отсюда вытекают равенства:
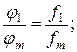
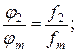 ….
…. 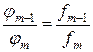 .
.
Из теоремы подобия вытекает важное следствие: все отношения между функциями 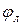 в любой из подобных систем не завися от преобразований подобия (являются инвариантами преобразования), т.е. не зависят от констант подобия
в любой из подобных систем не завися от преобразований подобия (являются инвариантами преобразования), т.е. не зависят от констант подобия 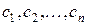 :
:
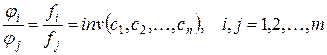 . (2.8)
. (2.8)
Отношения (2.8) называются инвариантами подобия.
Результаты теоремы, доказанной для случая двух систем, обобщаются и на случай 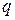 систем в виде:
систем в виде:
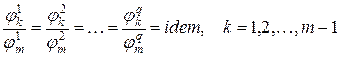 .
.
где idem означает «одинаково».
2.3. Преобразование подобия для моделей,
представленных дифференциальными уравнениям
Преобразования подобия математических моделей систем, представленных дифференциальными уравнениями, производят с целью перехода к другим масштабам величин (переменных и времени) при моделировании процессов. Особенно это актуально при использовании аналоговых вычислительных машин (АВМ), где модели реализуются в виде электронных схем из операционных усилителей. При моделировании на цифровых компьютерах это не столь актуально, однако и здесь иногда возникает необходимость масштабирования переменных и времени моделирования.
Рассмотрим модель в виде линейного однородного обыкновенного дифференциального уравнения с постоянными коэффициентами:
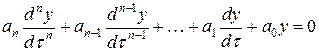 .
.
Для модели с теми же коэффициентами, но другими переменными, имеем:
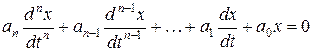
Преобразования подобия имеют вид: 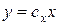 ,
, 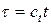 . После подстановки получаем подобную модель:
. После подстановки получаем подобную модель:
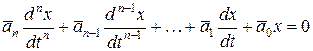 ,
,
где 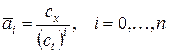 . Т.е., получена модель для масштабированных переменных и времен.
. Т.е., получена модель для масштабированных переменных и времен.
Применяя подобное преобразование ( 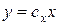 ,
, 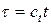 ) для неоднородной модели
) для неоднородной модели
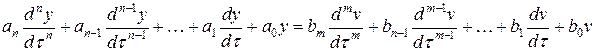 ,
,
получим модель
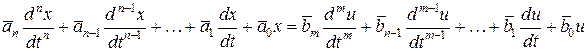 ,
,
где 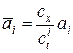 ,
, 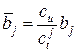 ,
, 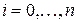 ,
, 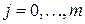 .
.
Дата добавления: 2016-04-02; просмотров: 653;
