Понятие моделирования
Моделирование – одна из категорий теории познания. В сущности, процесс познания и моделирование – почти синонимы.
Объект моделирования – произвольный предмет человеческой деятельности или природные явления. Примеры: устройство (самолет, корабль, электропривод), физическое явления (ядерная реакция, погода), процессы (экономика, биологические системы, технологический процесс). Различают материальные (вещественные), энергетические и информационные объекты моделирования.
В САМОМ ШИРОКОМ СМЫСЛЕ, МОДЕЛИРОВАНИЕ – ЭТО МЕТОДОЛОГИЯ НАУЧНОЙ И ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА, ОСНОВАННАЯ НА ИЗУЧЕНИИ СВОЙСТВ И ХАРАКТЕРИСТИК ОБЪЕКТОВ РАЗЛИЧНОЙ ПРИРОДЫ ПОСРЕДСТВОМ ЕСТЕСТВЕННЫХ ИЛИ ИСКУССТВЕННЫХ АНАЛОГОВ ОБЪЕКТОВ.
В более узком смысле, под моделированием понимают замещение обного объекта, называемого оригиналом или натурой, другим объектом, называемым моделью, которая позволяет фиксировать и изучать существенные свойства оригинала. Моделирование – это двуединый процесс создания модели и исследования модели. Модель всегда проще оригинала и отображает не все, а лишь основные характеристики оригинала. Для более полного исследования объекта обычно привлекают набор частных моделей. Пример для САУ: линейные модели, нелинейные модели, модели со случайными факторами и т.д. Использование комплекса моделей составляет принцип множественности (иерархии) моделей.
Сравнивая натурное и компьютерное моделирование, можно выявить следующие их черты:
| Натурный (физический) эксперимент | Вычислительный (компьютерный) эксперимент |
| Реальный объект (система) | Математическая модель |
| Средства измерений (меры, измерительный преобразователи, приборы) | Программные средства (языки программирования, пакеты программ) |
| Поверка средств измерения | Тестирование программных средств |
| Измерения величин и процессов | Моделирование прцессов |
Возможности натурного эксперимента ограничены как по возможностям, так и по стоимости. Например, затруднено моделирование аварийных ситуаций, приводящих к разрушению объекта (хотя иногда это практикуется: например, при проектировании самолетов обязательно один из экземпляров специально разрушается при проведении испытаний на прочность; тоже в автостроении – краш-тесты). Не всегда возможны испытания на людях. Некоторые натурные эксперименты требуют длительного времени. В таких случаях компьютерные эксперименты предпочтительнее, хотя их результаты сильно зависят от качества используемых моделей. Используется и полунатурное моделирование, когда в одном комплексе используются реальные объекты и математические модели (например, тренажеры-симуляторы). В настоящее время тенденция такова, что стараются чаще использовать компьютерное моделирование. Так, после запрещения испытаний ядерного оружия, все новые его виды проверяются только на моделях. Эти модели очень сложные и для их использования создаются суперкомпьютеры. Та же ситуация при разработке аэрокосмической техники.
Виды моделирования
Различают следующие виды моделирования
Натурное моделирование - специально поставленные исследования “на натуре”, т.е. в природе при специально созданных или подобранных условиях; результаты обрабатываются с помощью теории подобия; подгруппами данного вида моделирования являются
а) производственный эксперимент ,
б) обработка сведений о явлениях или процессах, естественно происходящих в натуре.
Примерами натурных моделей могут служить, в частности, природные и другие заповедники, испытательные полигоны и т. д.
Физическое моделирование - исследования проводятся на специальных установках, сохраняющих в основном природу явлений, но воспроизводящих их количественно иначе.
Примерами физических моделей являются масштабные модели самолетов в аэродинамических трубах, модели плотин гидроузлов и др.
Аналоговое моделирование - здесь физика исследуемого процесса не сохраняется и его изучение ведется на моделях другой физической природы.
Примером аналоговой модели является наборная схема какого-либо процесса на аналоговой вычислительной машине.
Идеальное (мысленное) моделирование осуществляют умозрительно, т.е. в сознании человека. Пример – мысленный эксперимент Галилея при открытии им независимости ускорения свободного падения от массы тела (пример с ядром и пулей, соединенных перемычкой).Идеальное моделирование реализуется в виде описательного и/или символического моделирования.
Символическое (знаковое) моделирование - здесь модели представляются различными знаковыми системами, фиксирующими различные знания о моделируемом объекте. Это могут быть словесные описания, описания на языке математики, описания в виде алгоритмов и т. д.
Математическое моделирование – частный случай знакового моделирование, когда описание производится на языке математики. При этом используются не только константы, переменные и математические действия, но и логические конструкции в виде условных операторов, циклов и прочих элементов записи алгоритмов и структур данных. При исследовании САУ широко используются следующие виды математических моделей: передаточные функции и структурные схемы в непрерывной (преобразование Лапласа) и дискретной (z-преобразование) формах; дифференциальные уравнения высоких порядков и системы дифференциальных уравнений первого порядка (нормальная форма Коши); дифференциальные уравнения с отклоняющимся аргументом (в частном случае – с запаздыванием); дискретные аналоги дифференциальных уравнений – конечно-разностные уравнения и их системы; гибридные системы, сочетающие подсистемы разного из перечисленных выше видов. Применяются также дифференциально-функциональные уравнения, включающие, помимо дифференциальных, нелинейные и/или трансцендентные уравнения. При описании систем с распределенными параметрами используются дифференциальные уравнения в частных производных и их дискретные аналоги (многоиндексные системы).
Для математических моделей введены понятия изоморфизма и гомоморфизма.
Изоморфными будут две такие системы объектов А и В с заданными в них отношениями, для которых выполняются следующие условия:
1) 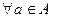 однозначно соответствует bÎ B и наоборот;
однозначно соответствует bÎ B и наоборот;
2) каждому отношению в А соответствует одно отношение в В и наоборот;
3) если некоторые объекты в А а1, а2, . . . связаны отношением R1(а1, а2, . . .), то в В соответствующие b1, b2, . . . связаны отношением R2(b1, b2, . . .).
Гомоморфными называют такие две системы А и В, между объектами которых нет взаимно-однозначного соответствия.
На практике изоморфные модели называют “адекватными”, а гомоморфные - “приблизительными”. Часто и изоморфные и гомоморфные модели называют адекватными, но при этом говорят о степени адекватности. Последняя характеристика не является количественной и вывод о степени адекватности модели обычно производится методом экспертных оценок. Следует отметить, что на практике изоморфные модели встречаются редко.
Дата добавления: 2016-04-02; просмотров: 786;
