ВВЕДЕНИЕ В ТЕОРИЮ ПОДОБИЯ
Основные понятия теории подобия
Пусть заданы система-оригинал 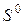 и система-модель
и система-модель  , которые характеризуются своими наборами элементов
, которые характеризуются своими наборами элементов 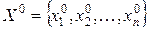 ,
, 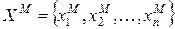 соответственно. Указанные наборы могут представлять собой любые переменные и/или параметры систем
соответственно. Указанные наборы могут представлять собой любые переменные и/или параметры систем 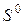 и
и  . Для этих систем определены уравнения связи:
. Для этих систем определены уравнения связи:
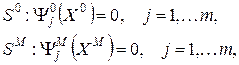 (2.1)
(2.1)
где  – операторы связи.
– операторы связи.
Если системы изоморфны (определение см. выше), то между ее элементами имеется взаимнооднозначное соответствие. Изоморфизм позволяет по свойствам модели изучать свойства оригинала. Изоморфные системы принято обозначать 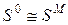 . Изоформизм обладает свойством транзитивности, т.е. из
. Изоформизм обладает свойством транзитивности, т.е. из 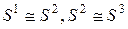 следует
следует  .
.
Пример.
Системы 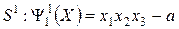 и
и 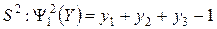 при постоянном
при постоянном 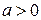 изоморфны. Для доказательства этого покажем взаимно-однозначное соответствие между ними. Если положить
изоморфны. Для доказательства этого покажем взаимно-однозначное соответствие между ними. Если положить  (соответственно,
(соответственно, 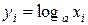 ), получим следующую цепочку преобразований:
), получим следующую цепочку преобразований: 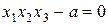 ,
, 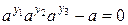 ,
, 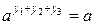 ,
, 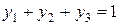 ,
, 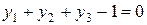 . Т.е., получено
. Т.е., получено 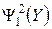 . Обратно, из
. Обратно, из 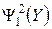 следует цепочка преобразований:
следует цепочка преобразований: 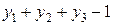 ,
, 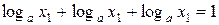 ,
, 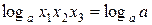 ,
,  ,
, 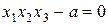 . В результате получено
. В результате получено 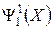 .
.
Среди изоморфных систем выделяют подобные системы, в которых связь между 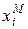 и
и  линейная вида
линейная вида 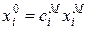 или
или  , где коэффициенты носят название коэффициентов или констант подобия или ассштабных коэффициентов.
, где коэффициенты носят название коэффициентов или констант подобия или ассштабных коэффициентов.
Построение подобных систем базируется на основных теоремах подобия.
Рассмотрим две системы, которые описывают уравнениями связи:
для  :
: 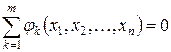 ; (2.2)
; (2.2)
для 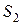 :
: 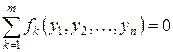 , (2.3)
, (2.3)
где 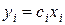 ,
,  .
.
Будем считать, что функции 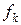 гомогенные (однородные) относительно своих параметров, т.е.:
гомогенные (однородные) относительно своих параметров, т.е.:
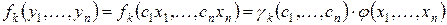 . (2.4)
. (2.4)
Примером гомогенной функции является функция 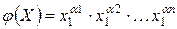 . Примером негомогенной функции является вида
. Примером негомогенной функции является вида  , если выражения под синусом двух синусоид не равны друг другу.
, если выражения под синусом двух синусоид не равны друг другу.
Дата добавления: 2016-04-02; просмотров: 666;
