Биологические триггеры. Силовое и параметрическое переключение триггера. Гистерезисные явления. Примеры.

Важная особенность биосистем – их способность переключаться из одного режима функционирования в другой, что соответствует нескольким устойчивым стационарным состояниям системы. Система, обладающая двумя или более стационарными состояниями, между которыми возможны переходы, называется триггерной

Рисунок 1

Переключение триггера из одного режима в другое возможно двумя способами: силовым и параметрическим.

При силовом способе мы изменяем значения переменных. Например, мы можем резко увеличить переменную х, Что переведёт систему в точку c’, откуда она самопроизвольно перейдёт в точку с (см. рисунок 1)

При параметрическом способе воздействуем на параметры (рН, изменение температуры, скорость поступления субстрата и др.). При этом изменяется фазовый портрет системы, зависящий от некоего управляющего параметра

Рисунок 2

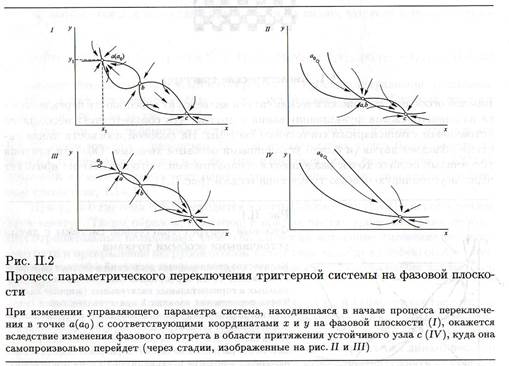
При возвращении к прежним значениям управляющего параметра исходный фазовый портрет системы восстановится, но сама система будет работать уже в другом режиме.

Примеры.

1.Система антагонистических видов

dx/dt = (x*АS)/(ks+S) – B*x – C*xy

dy/dt = (y*АS)/(ks+S) – B*y – C*xy

x – концентрация особей первого вида, y - концентрация особей второго вида, S – концентрация субстрата, А, В, С – константы. При взаимодействии оба вида погибают (последние члены в уравнениях). Субстрат лимитирует рост популяций

Здесь не включено отдельное уравнение для расходования субстрата, которое заменено алгебраическим:

dS/dt = So – (S*(x+y))/(ks+S)

Система представляет собой триггер, у которого две устойчивые точки расположены на координатных осях

Рисунок 3

2. Модель взаимной регуляции двух систем синтеза (дифференцировка клеток)

Рисунок 4

dx₁/dt = A1/(1+x₂ⁿ) – x₁

d x₂/dt = A2/(1+ x₁ⁿ) – x₂

x1 и x2 – безразмерные концентрации компрессоров продуктов Р1 и Р2. n – порядок реакций репрессии. А1 и А2 зависят от субстратов S1 и S2, активности и содержания ферментов базового метаболизма. (см рисунок 4)

При n = 1 система имеет одно стационарное решение (положительный корень для уравнения стационарных концентраций x² + x –A = 0)

При n = 2 число стационарных состояний равно числу положительных вещественных корней уравнения

A[1+A²/(1+x²)²]^-1 – x = 0

При А<2 есть всего одно решение x(стационар.)<1. Это устойчивая точка типа узла.

При А = 2 появляются три стационарных состояния, и система становится триггерной (это бифуркационное значение параметра, при котором устойчивый узел сменяется седлом)

В итоге, триггерный режим в этой системе возникает при участии в корепрессии 2 и более молекул продукта, и при высоком уровне базового метаболизма.

3. Открытая ферментативная система с субстратным угнетением – включает в себя реакцию притока субстрата, оттока продукта и образование неактивного комплекса.

So→^k S +E _k-1↔^k1 ES →^k2 E+P →^k4

ES + S _k-3↔^k3 ES²

Скорость образования продукта в данной схеме:

υ_p = (k2*Eo*S)/(Km +S+[S²/ks]), где ks = k3/k-3

При S<<1 величиной S²/ks можно пренебречь – уравнение совпадает с уравнением Михаэлиса-Ментен. При S→ ∞ образуется неактивный комплекс и υ_p→0.

Скорость изменения концентрации субстрата S складывается из скорости притока (υ_прит=k(So –S) = α – kS) и оттока в ходе ферментативной реакции:

υ_s = υ_прит - υ_p

В стационарном состоянии υ_прит - υ_p = 0

Стационарные точки S являются пересечением кривых υ_p(S) и υ_прит (S)

Рисунок 5

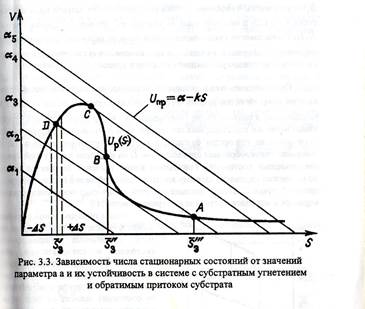
В интервале α2< α < α4 система имеет три различных стационарных состояния, а значения α2 и α4, при которых изменяется число стационарных точек, являются бифуркационными.

Проверим устойчивость точек. Зададим смещение от точки S3’ влево. Мы видим, что скорость притока субстрата стала больше скорости его оттока (тонкая линия над толстой кривой). При смещении вправо наоборот υ_p(S) > υ_прит (S)=> система стремиться вернуться в эту точку. Аналогично находим, что S3’’ неустойчива, а S3’’’ – устойчива. Устойчивые точки расположены на кривой υ_p(S) на участках AB и CD, а неустойчивые – на участке BC

Построим график зависимости стационарных состояний от управляющего параметра α:

Рисунок 6

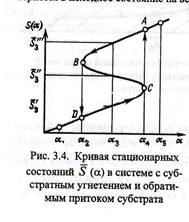
Здесь есть два устойчивых участка – система может работать в двух режимах. При попадании на неустойчивый участок система совершает перескок (см направление стрелок на рисунке) Таким образом, система является триггерной. Направление переходов и реализация одного или другого устойчивого состояния зависят от того, происходит ли увеличение или уменьшение параметра (по какой ветке движется система). Это свойство системы – совершать разными путями переход из одного состояния в другое в зависимости от предыстории системы называется гистерезисом.Периодическое движение вдоль гистерезисного цикла носит колебательный характер: A→B→D→C→A