Цепь синусоидального тока с индуктивным сопротивлением.

| Известно, что переменный ток, проходя через катушку индуктивности, вызывает ЭДС самоиндукции 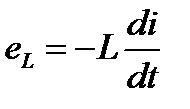 , где , где 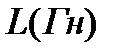 - индуктивность. - индуктивность.
|
Эта ЭДС уравновешивается приложенным напряжением:
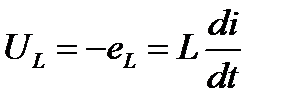
Пусть 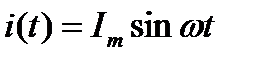 (полагаем
(полагаем 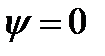 ).
).
Тогда 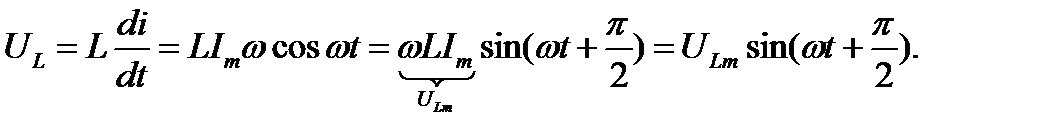
Графики мгновенных значений тока и напряжения на индуктивности имеют вид:
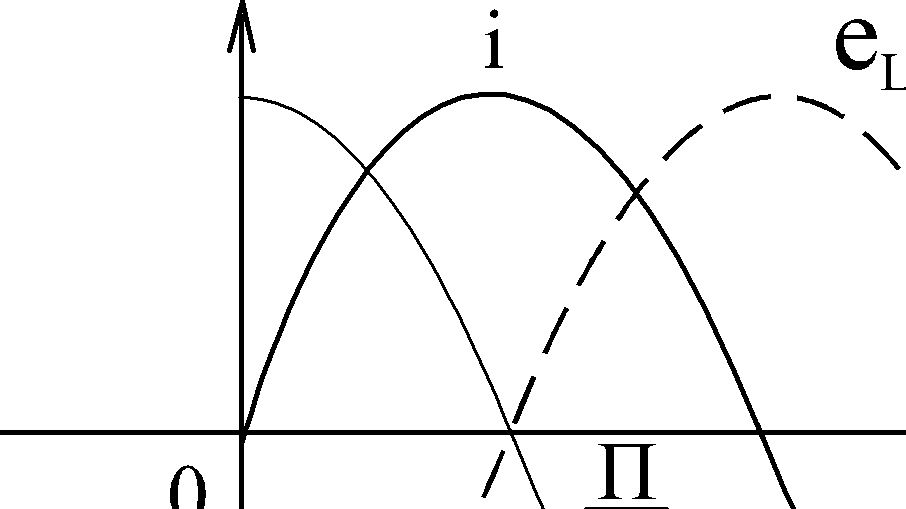
| Таким образом, разность фаз напряжения и тока на индуктивном элементе составляет 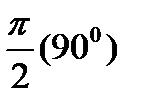 , причем кривая тока отстает от кривой напряжения. , причем кривая тока отстает от кривой напряжения.
|
Запишем действующее значение напряжения:
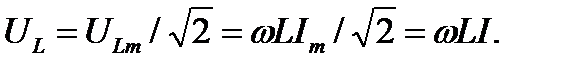
Величину 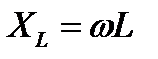 назовем индуктивным сопротивлением. Тогда получим закон Ома для индуктивной цепи:
назовем индуктивным сопротивлением. Тогда получим закон Ома для индуктивной цепи:
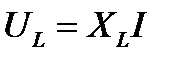
Запишем комплексные значения тока и напряжения:
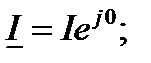
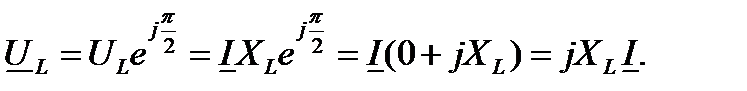
Величина 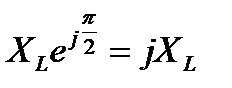 называется комплексным индуктивным сопротивлением. Следовательно, может быть записан для индуктивной цепи закон Ома в комплексной форме:
называется комплексным индуктивным сопротивлением. Следовательно, может быть записан для индуктивной цепи закон Ома в комплексной форме:
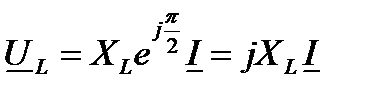
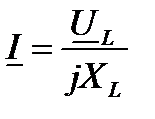 .
.
Векторная диаграмма цепи имеет вид:
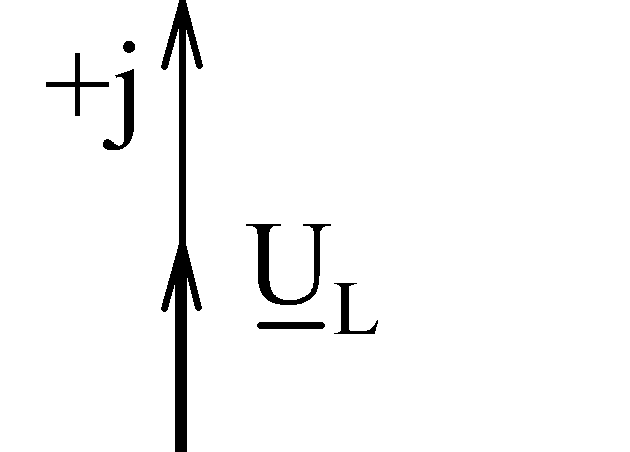
| На диаграмме видно, что вектор тока, протекающий через индуктивный элемент, отстает от вектора напряжения на нем (считая, что векторы вращаются против часовой стрелки). |
Таким образом, если 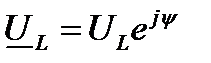 , то
, то 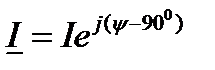
Найдем выражение для мгновенной мощности индуктивной цепи:
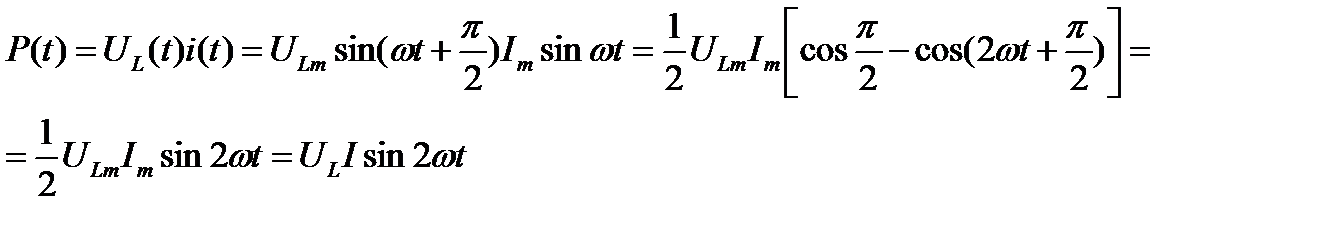
График 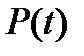 имеет вид:
имеет вид:

| Из графика видно, что активная мощность, равная среднему значению мгновенной мощности, равна нулю, т.е. индуктивный элемент активную мощность не потребляет. |
Для реактивных элементов вводится понятие реактивной мощности, равной амплитудному значению мгновенной мощности:
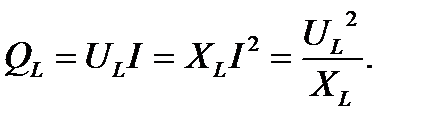
Размерность для реактивной мощности та же, что и для активной, но чтобы их различать, единица реактивной мощности называется "вар" (вольт-ампер-реактивный).
Дата добавления: 2016-02-16; просмотров: 819;
