Законы Ома и Кирхгофа в комплексной форме.

Закон Ома в комплексной форме получаем из формулы для комплексного сопротивления:

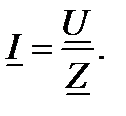
По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:

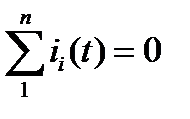
Равенство не нарушится, если вместо токов подставить соответствующие комплексы. Это и будет выражение для первого закона Кирхгофа в комплексной форме:

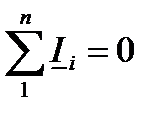
где 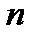- количество ветвей, подходящих к узлу.

По второму закону Кирхгофа, в любом (замкнутом) контуре справедливо равенство алгебраических сумм мгновенных значений напряжений на сопротивлениях контура и ЭДС:

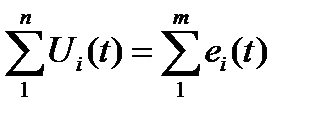
Заменив напряжения и ЭДС на соответствующие комплексы, получим выражение для второго закона Кирхгофа в комплексной форме:

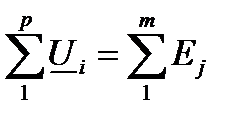
где 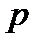- количество элементов в контуре,

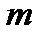- количество ЭДС в контуре.

Пример:

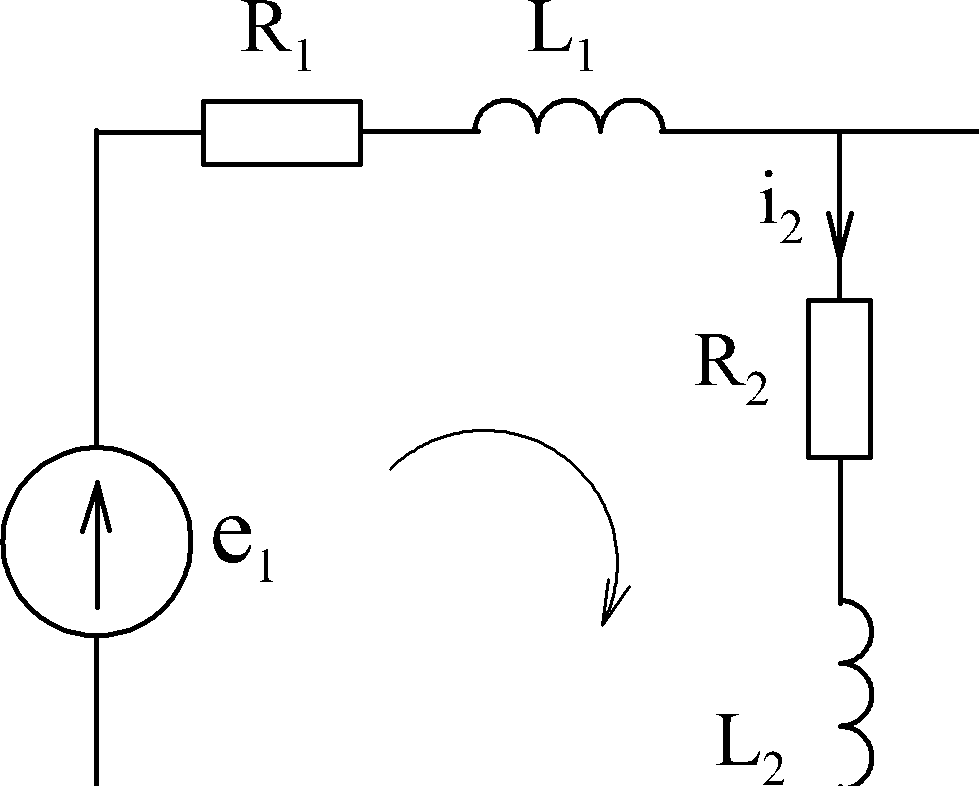
В качестве потребителей электрической энергии в цепях переменного тока используются самые различные технические устройства, число их велико, но в схемах замещения, отражающих явления, происходящие в цепях, мы будем использовать три типа идеальных элементов.

а) резисторный элемент

Этот элемент обладает только активным сопротивлением и отражает необратимый процесс поглощения энергии (преобразование энергии в тепловую).

б) индуктивный элемент

Это идеальная катушка, активное сопротивление провода которой принимается равным нулю. Этот элемент отражает свойство катушки создавать магнитное поле.

в) емкостной элемент

Это идеальный конденсатор, не имеющий токов утечки. Этот элемент отражает свойство накопления зарядов или создания электрического поля.