Цепь синусоидального тока с емкостным сопротивлением.

| Пусть 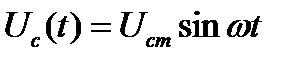 (полагаем (полагаем 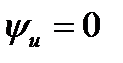 )
Ток через емкость пропорционален скорости изменения заряда. )
Ток через емкость пропорционален скорости изменения заряда.
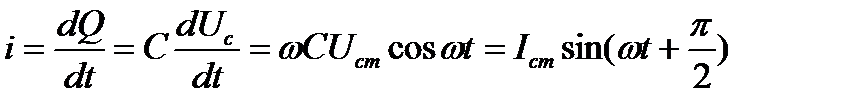 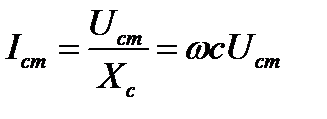
|
Графики  и
и  имеет вид:
имеет вид:
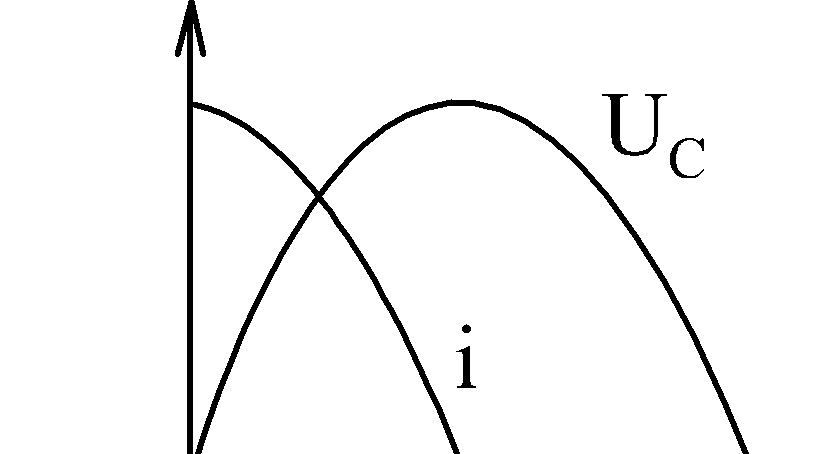
|
Для емкостной цепи кривая тока опережает кривую напряжения на четверть периода 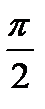 . .
|
Таким образом, если 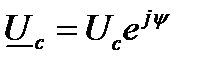 , то
, то 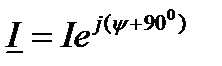
Закон Ома в комплексной форме для емкостного элемента имеет вид:
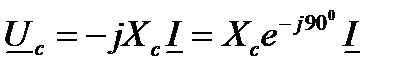
Величина 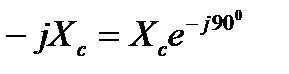 называется комплексным емкостным сопротивлением.
называется комплексным емкостным сопротивлением.
Активная мощность емкостной цепи так же, как и для индуктивной равна нулю, а реактивная мощность определяется выражением:
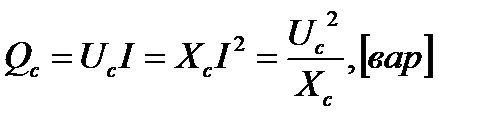
Векторная диаграмма цепи имеет вид:
Рассмотрим цепь с последовательным соединением  и
и  (рис.14).На зажимы А и Д подано синусоидальное напряжение.
(рис.14).На зажимы А и Д подано синусоидальное напряжение.
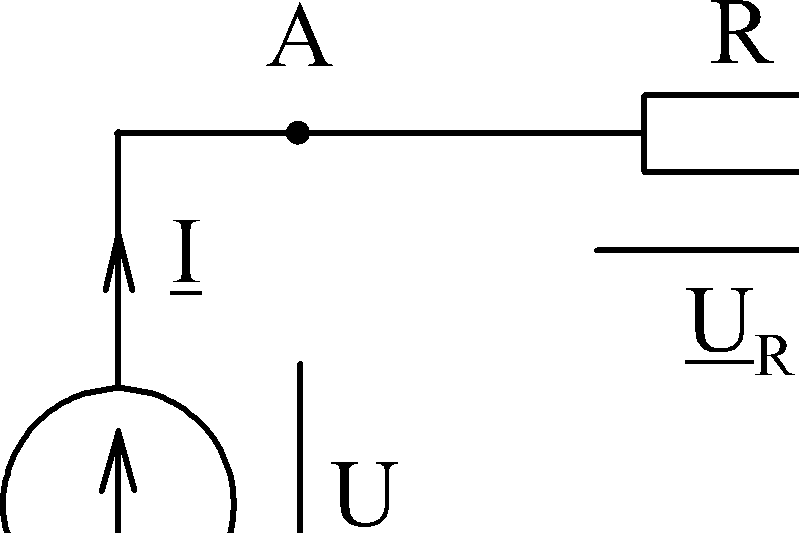 Рис.14
Рис.14
| Согласно 2-му закону Кирхгофа в комплексной форме справедливо уравнение:
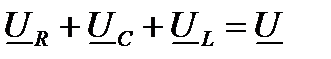 где
где 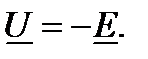 Или
Или
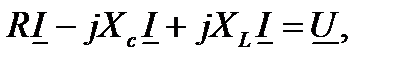
|
которое удобно представить в виде 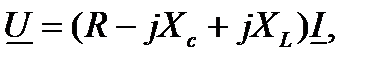
где 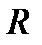 - активное сопротивление (всегда положительно),
- активное сопротивление (всегда положительно),
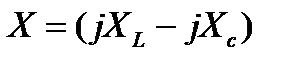 - реактивное сопротивление.
- реактивное сопротивление.
Тогда 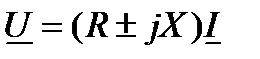
При знаке "+" цепь носит индуктивный характер, при знаке "-" - емкостной характер.
Запишем комплексное сопротивление в показательной форме
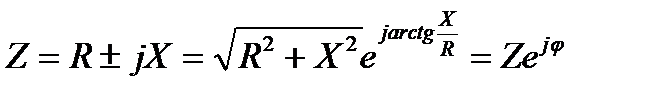
где 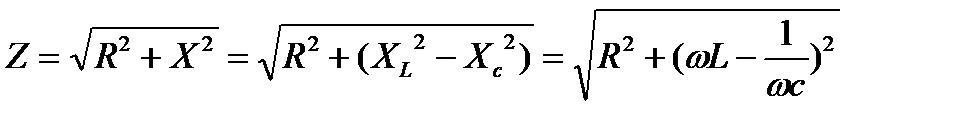
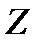 - полное сопротивление, модуль комплексного сопротивления,
- полное сопротивление, модуль комплексного сопротивления,
 - аргумент комплексного сопротивления
- аргумент комплексного сопротивления

Угол  - угол сдвига фаз между напряжением и током.
- угол сдвига фаз между напряжением и током.
В справедливости вышеприведенных выражений легко убедиться, если изобразить комплексное число 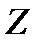 вектором на комплексной плоскости.
вектором на комплексной плоскости.

| Треугольник, образованный векторами
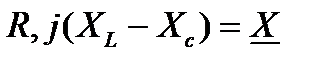 и и 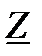 , называется треугольником сопротивлений.
Удобно пользоваться следующими выражениями: , называется треугольником сопротивлений.
Удобно пользоваться следующими выражениями:
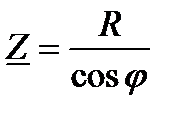 ; ; 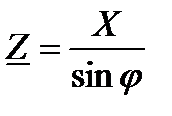
|
Дата добавления: 2016-02-16; просмотров: 949;
