Параллельные цепи синусоидального тока.

Рассмотрим схему цепи, состоящей из трех параллельно соединенных ветвей (рис.19).

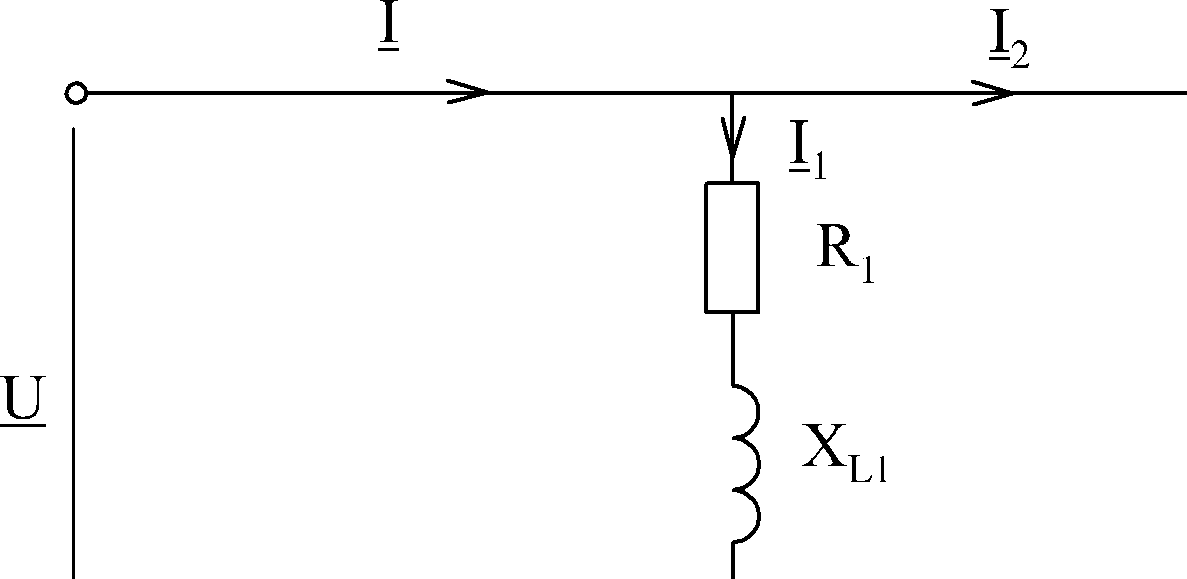
Рис.19

В соответствии с первым законом Кирхгофа в комплексной форме можем записать:

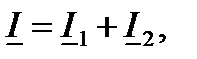
или

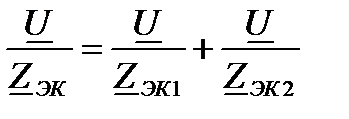
где 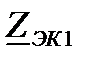и - эквивалентные комплексные электрические сопротивления ветвей;

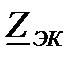- эквивалентное комплексное электрическое сопротивление цепи.

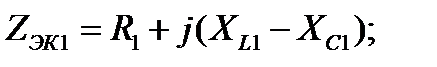
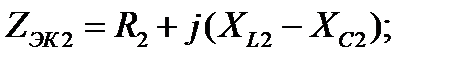
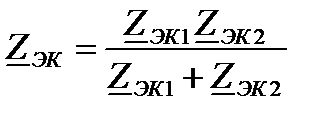
Напряжение на входных зажимах цепи

.

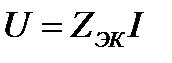Проводимость цепей синусоидального тока.

Рассмотрим электрическую цепь, состоящую из параллельно соединенных элементов 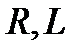и 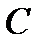(рис.20).

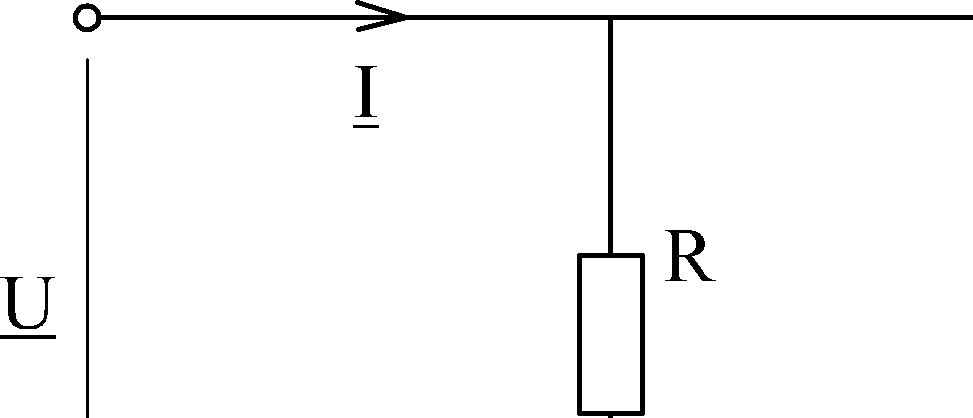
Рис.20

В соответствии с первым законом Кирхгофа в комплексной форме получим:

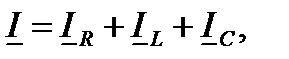
где токи в отдельных элементах можно определить, используя комплексные проводимости:

; ;

.

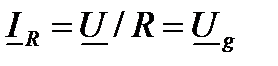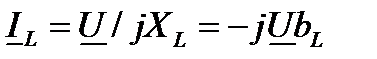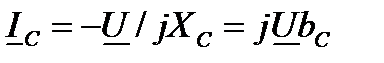Общая комплексная проводимость цепи:

;

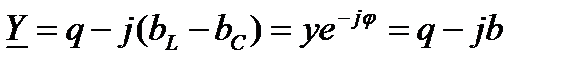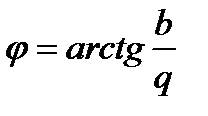
где 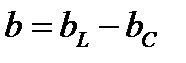- общая реактивная проводимость.

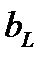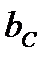Как видно, в зависимости от соотношения проводимостей и , общий ток 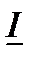может иметь индуктивный 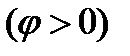, емкостной 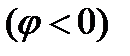и чисто активный характер .

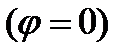Случай, когда 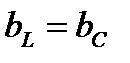, соответствует, так называемому, резонансу токов.

Резонанс токов.

Режим цепи при параллельном соединении элементов 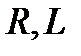и 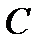, когда индуктивная и емкостная проводимости равны, а токи в ветвях с реактивными проводимостям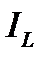и и 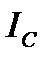равны по значению и могут превышать полный ток цепи, называется режимом резонанса токов.

При этом общий ток в цепи имеет минимальное значение:

.

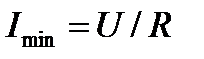Случаю резонанса соответствует резонансная частота:

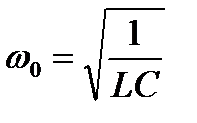
При резонансе токов реактивные процессы ограничиваются лишь контуром из элементов 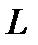и 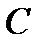, общий ток цепи совпадает по фазе с напряжением, т.е. является чисто активным.

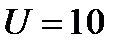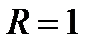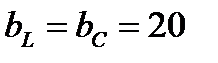Пример: Пусть В, Ом, Ом.

Имеем резонанс токов, общий ток минимален:

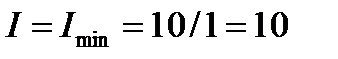А.

Определяем токи в реактивных элементах:

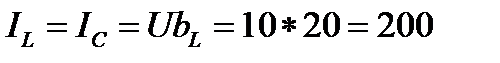A;

как видно, .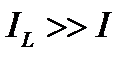

Для иллюстрации фазовых соотношений между токами и напряжением строим векторные диаграммы на комплексной плоскости для случая резонанса 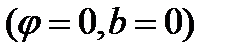и для случая 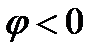, когда сопротивление цепи имеет емкостной характер и общий ток опережает по фазе входное напряжение.

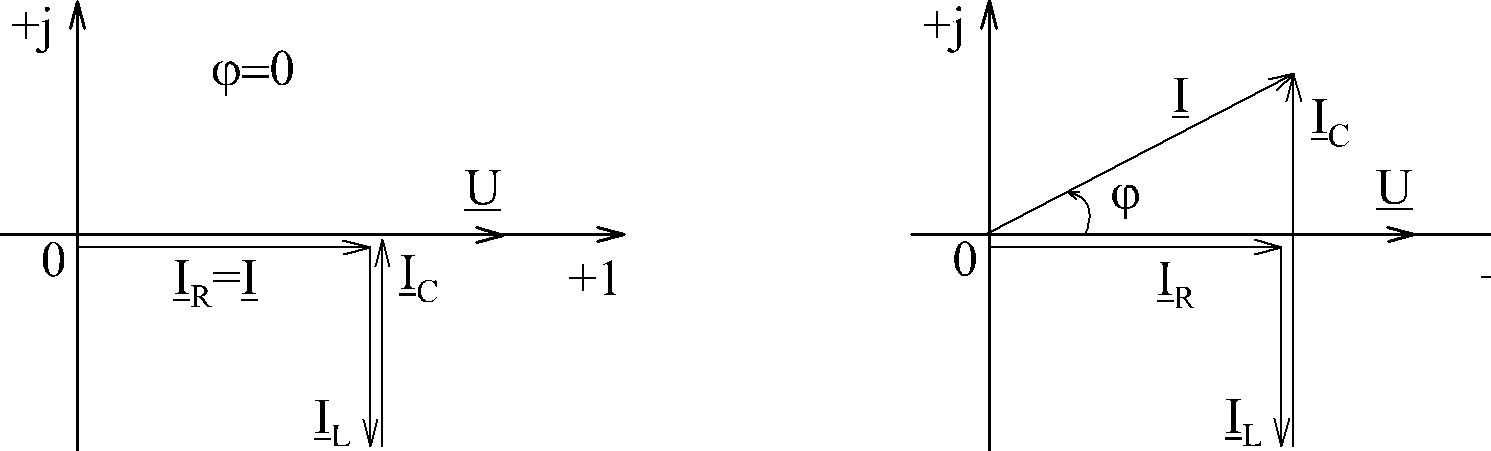
Как видно, при резонансе токов векторы токов в реактивных элементах равны по величине и противоположны, т.е. компенсируют друг друга.