Представление синусоидальных электрических величин временными диаграммами, векторами и комплексными числами.

Синусоидальные ЭДС, напряжения и токи можно изображать графически в виде соответствующих синусоид, такие графики в электротехнике называют волновыми диаграммами (см. рис. 13).

Обычно на одной волновой диаграмме изображают несколько синусоид переменных величин (напряжений, токов), относящихся к одной и той же цепи. Для оценки их взаимного расположения вдоль оси абсцисс вводится разность их начальных фаз, называемая фазовым сдвигом. Чаще всего встречается фазовый сдвиг между током и напряжением.

Если 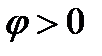, то говорят, что напряжение опережает ток по фазе, при напряжение отстает по фазе от тока, при напряжение и ток совпадают по фазе, а если 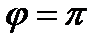, то напряжение и ток находятся в противофазе.

Волновые диаграммы не всегда удобны для исследования, особенно при сложных разветвленных цепях. Проще в этом случае изображать синусоидальные величины вращающимися векторами. Изобразим вращающийся вектор, соответствующий току:

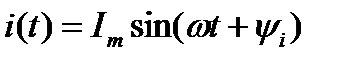
Длина отрезка ОА в принятом масштабе равна амплитуде тока . Проекция вектора на ось ординат (ОВ) равна мгновенному значению тока в момент времени . При вращении вектора в положительном направлении (т.е. против часовой стрелки) с угловой скоростью в любой момент времени его проекция на ось ординат будет равна соответствующему мгновенному значению тока:

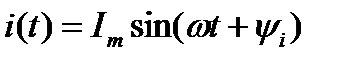
Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка 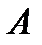на рисунке).

Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.

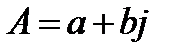
Представленная форма записи называется алгебраической формой комплексного числа.

Кроме алгебраической существует показательная форма записи комплексного числа:

где - модуль (длина) вектора

- поворотный множитель

- аргумент, т.е. угол, на который повернут вектор в положительном направлении относительно вещественной оси.

Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:

;

;

При сложении и вычитании комплексных чисел удобно пользоваться алгебраической формой записи:

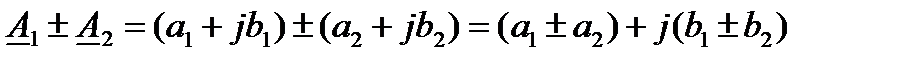
При умножении, делении, возведении в степень удобно пользоваться показательной формой

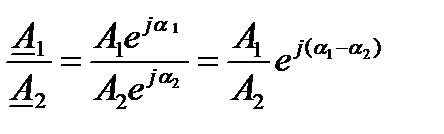
Если комплексное число 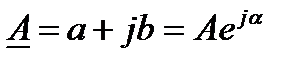, то комплексное число называется сопряженным комплексным числом.

Синусоидальное ЭДС можно представить комплексным числом:

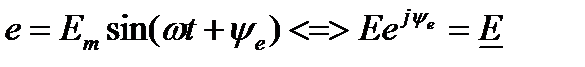
Для напряжения и тока аналогично.

При расчетах цепей синусоидального тока целесообразно перейти от гармонических функций времени к их изображениям в комплексной форме и производить все расчеты, используя комплексные числа. Конечный результат может быть представлен снова в виде синусоидальной функции времени.