Целесообразность введения числовой характеристики рассеяния случайной величины

Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но разные возможные значения. Рассмотрим, например, дискретные случайные величины X и Y, заданные следующими законами распределения:

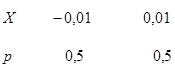
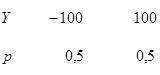
Найдем математические ожидания этих величин:

,

.

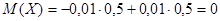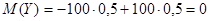Здесь математические ожидания обеих величин одинаковы, возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.

По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.

Прежде чем перейти к определению и свойствам дисперсии, введем понятие отклонения случайной величины математического ожидания.