Методические пояснения и рекомендации. По изучению второго вопроса.
По изучению второго вопроса.
1.Для заданий №1, 3, 4, 5 п. 1 вычислить дисперсию распределения случайной величины Х.
2.Случайная величина Х задана законом распределения
| Х | |||
| р | 0,1 | 0,4 | 0,5 |
Найти среднее квадратичное отклонение 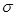 (X).
(X).
3.Найти дисперсию дискретной случайной величины Х – числа появления события А в пяти независимых испытаниях, если вероятность появления событий А в каждом испытании равна 0,2.
4.Брошены nигральных костей. Найти дисперсию суммы числа очков, которые могут появиться на всех выпавших гранях.
Рекомендуемая литература
1. Боровков А.А. Теория вероятностей. - М., "Эдиториал УРСС", 2009.
2. Теория вероятностей: Учебник для вузов. 2-е изд./ А.В. Печинкин, О.И. Тескин, Г.М. Цветкова и др.; Под редакцией В.С. Зарубина, А.П. Крищенко. –, стереотип. – М.: Изд-во МГТУ им. Баумана, 2001. – 456 с. (Сер. Математика в техническом университете; Вып. XVI).
3. Вентцель Е.С., Овчаров Л.А Задачи и упражнения по теории вероятностей. Учеб. пособие для втузов. – М., Высш. шк., 2010.
Практическое занятие № 6
Тема: «Числовые характеристики непрерывных случайных величин»
Цель работы:
1. Изучить числовые характеристики непрерывных случайных величин и их свойства.
2. Используя формулы числовые характеристики непрерывных случайных величин уметь определять математическое ожидание и дисперсию.
3. Выработать навыки в использовании формул математического ожидания и дисперсии.
4. Приобрести навыки в проведении математических расчётов.
Учебные вопросы
1. Дисперсия дискретной случайной величины
2. Математическое ожидание дискретной случайной величины
3. Заключение
4. Задание студентам для самостоятельной работы
Время, отводимое на занятие – 80 мин.
Проверка готовности студентов к занятию
1. Какая случайная величина называется непрерывной?
2. Что называется плотностью распределения вероятностей?
3. Что называется математическим ожиданием непрерывной случайной величины?
4. Дать определение дисперсии непрерывной случайной величины?
5.Дать определение начального теоретического момента порядка k?
6.Дать определение центрального теоретического момента порядка k?
Дата добавления: 2016-03-27; просмотров: 883;
