По выполнению первого вопроса. 1.Дискретная случайная величина Х задана законом распределения
1.Дискретная случайная величина Х задана законом распределения
А)
| Х | ||||
| р | 0,2 | 0,1 | 0,4 | 0,3 |
Б)
| Х | ||||
| р | 0,3 | 0,1 | 0,2 | 0,2 |
В)
| Х | |||
| р | 0,1 | 0,7 | 0,2 |
Вычислить математическое ожидание.
2.Найти математическое ожидание дискретной случайной величиныZ, если известны математические ожидания X и Y: а) Z=X+2Y, M(X)=5, M(Y)=3; б)Z=3X+4Y, M(X)=2, M(Y)=6.
3.Дискретная случайная величина Х принимает три возможных значения x 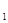 =4с вероятностью p
=4с вероятностью p 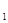 =0.5; x
=0.5; x 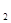 =6с вероятностью p
=6с вероятностью p 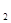 = 0.3; x
= 0.3; x 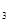 с вероятностью p
с вероятностью p 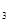 . Найти x
. Найти x 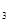 и p
и p 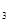 , зная, что M(X)=8.
, зная, что M(X)=8.
4.Контрольная работа состоит из трёх вопросов. На каждый вопрос приведено по 4 ответа. Составить и изобразить графически закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание этой случайной величины.
5.В билете 3 задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8, третьей – 0,7. Составить и изобразить графически закон распределения числа правильного решения задач в билете и вычислить математическое ожидание этой случайной величины.
6.Сделано два высокорисковых вклада: 10 тыс. рублей в компанию А и 15 тыс. рублей в компанию В. Компания А обещает 50% годовых, но может лопнуть с вероятностью 0,2. Компания В – 40% годовых, но может лопнуть с вероятностью 0,15. Составить закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год. Найти её математическое ожидание.
7.Найти математическое ожидание лотерейных билетов, на которых выпадут выигрыши, если приобретено 20 билетов, при чём вероятность выигрыша по одному билету составляет 0,3.
8.Найти математическое ожидание дискретной случайной величины Х, распределённой по закону Пуассона:
| X | 0 | 1 | 2 | k |
| p | exp(-λ) | 
| 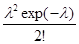
| 
|
Учитывать, что 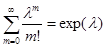
Дата добавления: 2016-03-27; просмотров: 1606;
