По выполнению первого вопроса. 1.Случайная величина Х задана плотностью распределения f(x)=x/2 в интервале (0, 2); вне этого интервала f(x)=0

1.Случайная величина Х задана плотностью распределения f(x)=x/2 в интервале (0, 2); вне этого интервала f(x)=0. Найти математическое ожидание величины Х.

2.Случайная величина Х задана плотностью распределения 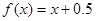в интервале (0;1); вне этого интервала f(x)=0. Найти математическое ожидание функции 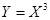(не находя предварительно плотности распределения Y).

3.Найти математическое ожидание случайной величины Х, заданной функцией распределения:

4.Случайная величина Х задана плотностью вероятности f(x)= 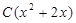в интервале (0;1). Вне этого интервала f(x)=0. Найти параметр С?

5.Случайная величина Х на интервале (2, 4) задана плотностью распределения f(x)= -(3/4)x +(9/2)x-6; вне этого интервала f(x)=0. Найти моду, математическое ожидание и медиану величины Х.

6.Функция 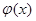задана в виде:

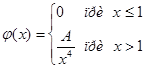
Найти:

а) значение постоянной А, при которой функция будет плотностью вероятности некоторой случайной величины Х;

б) выражение функции распределения F(x);

в) вычислить вероятность того, что случайная величина Х примет значение на отрезке [2;3];

г) найти математическое ожидание и дисперсию случайной величины Х.