Математическое ожидание числа появлений события в независимых испытаниях

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Чему равно среднее число появления события А в этих испытаниях? Ответ на этот вопрос дает следующая теорема.

Теорема. Математическое ожидание М(X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

.

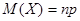Доказательство. Будем рассматривать в качестве случайной величины X число наступления события А в n независимых испытаниях. Очевидно, общее число X появления события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х₁ – число появлений события в первом испытании, X₂ - во втором, ..., Х_n – в n-м, то общее число появлений события Х = Х₁ + Х₂+...+Х_n.

По третьему свойству математического ожидания,

. (*)

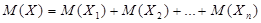Каждое из слагаемых правой части равенства есть математическое ожидание числа появлений события в одном испытании: М(Х₁) – в первом, М (X₂)- во втором и т. д. Так как математическое ожидание числа появлений события в одном испытании равно вероятности события (см. § 2, пример 2), то М(Х₁)=М(Х₂)=М(Х_n)=р Подставляя в правую часть равенства (*) вместо каждою слагаемого р, получим

. (**)

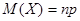Замечание. Так как величина X распределена по биномиальному закону, то доказанную теорему можно сформулировать так: математическое ожидание биномиального распределения с параметрами n и р равно произведению nр.

Пример. Вероятность попадания в цель при стрельбе из орудии p=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание

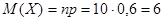(попаданий).

Задачи

1. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:

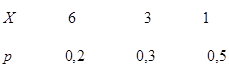
Ответ 2,6

2. Производится 4 выстрела с вероятностью попадания в цель р₁=0,6, р₂=0,4, р₃=0,5 и р₄ = 0,7. Найти математическое ожидание общего числа попаданий.

Ответ 2,2 попадания.

3. Дискретные независимые случайные величины заданы законами
распределения:

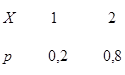
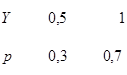
Найти математическое ожидание произведения XY двумя способами: а) составив закон распределения XY; б) пользуясь свойством 3.

Ответ 1,53.

4. Дискретные случайные величины X и Y заданы законами распределения, указанными в задаче 3. Найти математическое ожидание суммы Х+Y двумя способами: а) составив закон распределении Х+Y; б) пользуясь свойством 4.

Ответ 2,65.

5. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.

Ответ 2 детали.

6. Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей.

Ответ 12,25 очка.

7. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по одному билету равна 0,3.

Ответ 6 билетов.