Послідовність математичної обробки експериментальних даних

Cхемa обробки результатів спостереження є наступною:

а) визначення середнього значення отриманих результатів, тобто обчислення середньої арифметичної 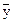за формулою:

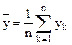(6.12)

б) визначення відхилення від середнього значення для кожного результату за формулою:

(6.13)

Ці відхилення характеризують абсолютну помилку визначення.

Випадкові помилки мають різні знаки. Коли значення результату досліду перевищує середнє значення, помилка досліду вважається позитивною. Коли ж значення результату досліду менше середнього значення, помилка вважається негативною. Чим точніше проведені виміри, тим ближче значення окремих результатів і середнє значення

в) обчислення дисперсії 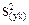за формулою:

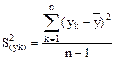(6.14)

г) обчислення стандартного відхилення окремого значення за формулою:

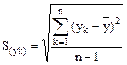(6.15)

і стандартного відхилення середнього результату за формулою (6.18)

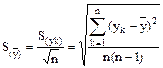(6.16)

д) перевірка надійності отриманих результатів за критерієм Стьюдента ta для проведеної кількості дослідів n при обраній надійній імовірності α. У більшості випадків при хіміко-технологічних дослідженнях приймають а = 0,95 або 0,99.

Це означає, що 95 % або 99 % абсолютних відхилень результатів лежать в означених межах.

Критерій t_a з надійною ймовірністю а показує, у скільки разів модуль різниці між істинним значенням величини у, що визначається, і середнім значенням менше стандартного відхилення середнього результату відповідно (6.19).

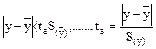(6.17)

Знайшовши за таблицею значення t_a та використовуючи раніше отримане значення , розраховують помилку отриманого середнього результату .

е) Встановлення інтервалу, в якому з надійною ймовірністю буде знаходитися середній результат .

ж) Визначення відносної помилки за формулою:

(6.18)

Якщо значення велике порівняно зі значенням y, то результати, що обробляються, перевіряють за одним з вищеописаних способів (за критерієм максимального відхилення Стьюдента або t_a на наявність грубих помилок. Для такої перевірки можуть застосовуватися й інші методи.

Після виключення грубих помилок проводиться вторинна обробка за такою ж схемою, але вже без виключених експериментальних даних.

Розглянемо приклад математичної обробки результатів дослідження.

У результаті визначення змісту мальтози у пивному суслі отримано 5 значень (у_k). Розмістимо ці значення в порядку зростання їхньої величини і запишемо у графу 2 таблиці 6.16. Після цього зробимо обробку результатів за приведеним вище алгоритмом.

Визначимо середній результат

Розрахуємо відхилення від середнього для кожного результату
і запишемо їх у графу 4 табл. 6.1. Після цього розрахуємо квадрати цих
відхилень і запишемо в графу 5 цієї ж таблиці.

Таблиця 6.1 - Таблиця математичної обробки результатів експерименту

п	Первинна обробка	Вторинна обробка
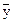
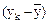
yk				yk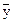
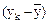
	7,52	7,24	+ 0,28	0,0784	7,4	0,12		0,0144
	7,50	+ 0,26	0,0676	0,10		0,01
	7,48	+ 0,24	0,0576	0,08		0,0064
	7,10	- 0,14	0,0196	- 0,3		0,09
	6,60	- 0,6	0,4096
Сума	36,2		0,6328			0,1208

Розрахуємо стандартне відхилення окремого виміру і середнього результату:

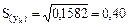
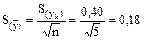
Визначимо величину надійної помилки . Для цього за таблицею 1 додатка А знаходимо значення критерію Стьюдента при надійній імовірності α = 0,95 і числі ступенів свободи f = n - 1 = 5 – 1 = = 4

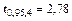
Встановлюємо інтервал, в якому з надійністю α = 0,9 знаходиться середній результат 7,24 ±0,50.

Визначаємо відносну помилку:

Відносна помилка визначення є великою.

При розгляді результатів досліду з табл. 6.2 (графа 2) видно, що останнє значення сильно відрізняється від інших. Перевіримо, чи не є воно грубою помилкою. Для цього користуємося критерієм Стьюдента.

Оскільки п'ятий результат досліду поставлено під сумнів, виключимо його і розрахуємо для чотирьох, що залишалися, 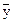і :

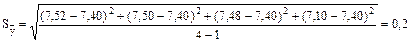
Розрахункове значення критерію Стьюдента:

Табличне значення цього критерію при α = 0,95 і f = 3, t_Т = 4,304 за таблицею А1 додатка А.

Порівнюючи ці значення, бачимо, що t_р < t_Т, отже, сумнівний результат не можна вважати грубою помилкою.

Повторимо математичну обробку для результатів експерименту, які залишилися після виключення грубої помилки.

Середній результат 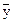= 7,40.

Відхилення від середнього для кожного результату наведені в таблиці 6.16 (графа 3 вторинної обробки).

Дисперсія окремого виміру:

Стандартні відхилення:

;

Величина надійної помилки 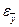. Знайдемо значення критерію
Стьюдента при α = 0,95 і f = n - 1 = 4 - 1 = 3;

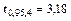
Надійний інтервал 7,40 + 0,32;

Відносна помилка:

Перевіримо значення у₄ = 7,40, чи не є воно грубою помилкою. Для цього використаємо перші три результати експерименту.

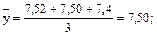
Із додатка А маємо:

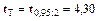
t_р > t_Т,

Результат у₄ = 7,40 також є грубою помилкою. Тому математичну обробку слід проводити за результатами вимірювань у₁, у₂, у₃.