Визначення необхідної кількості повторних дослідів

Для одержання істинного значення параметра у, що вимірюється із заданим надійним інтервалом 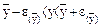необхідно проводити дослід із визначеним числом повторень. Звичайно буває достатнім прийняти 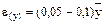і надійну ймовірність а = 0,95, рідше 0,99.

Розв’язок цієї задачі може бути здійснено різними методами, це залежать від того, чи має дослідник у своєму розпорядженні істинне значення середньоквадратичного відхилення δ, його експериментальну оцінку 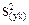, чи цю оцінку потрібно ще одержати, провівши відповідний експеримент.

Як приклад, що зустрічається найбільш часто, розглянемо випадок визначення необхідної кількості повторних дослідів для одержання результатів із заданою точністю.

Нехай необхідно встановити, скільки дослідів потрібно провести при визначенні якогось показника, щоб середній результат мав точність не нижче заданої. Для розв'язку такої задачі спочатку знаходять 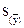із невеликої (2-3) кількості дослідів. Далі задають деяку надійну ймовірність (звичайно а = 0,95) та необхідне значення величини 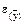, тобто відхилення середнього результату 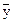від істинного значення величини у, яку визначаємо.

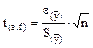(6.7)

Після цього за допомогою таблиці і розрахунків підбирають таку кількість дослідів (n), щоб критерій Стьюдента t_(α,f) при f = n - 1 відповідав розрахованому.

Якщо отримане значення п дуже велике, то одержання заданої точності визначення у прийнятим методом експерименту є нераціональним. Варто застосувати інший, більш точний метод.

Приклад. Припустимо, що в результаті досліду отримано два значення: 49,8 і 50,2. Потрібно визначити необхідну кількість повторних дослідів, щоб забезпечити при надійній імовірності а = 0,95 точність середнього результату (відносну помилку) у 1,0 %.

Обчислюємо статистичні характеристики.

Середній результат:

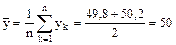
Дисперсія окремогрезультату:

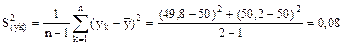
Середньоквадратична помилка окремого результату:

Середньоквадратична помилка середнього результату:

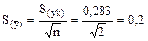
Із таблиці [3,6,7] для а = 0,95 і f = n - 1 = 1 знаходимо t _{0,95; l} = 12,7.

Величина надійної помилки (абсолютна похибка):

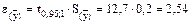
Відносна помилка:

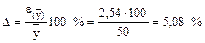
Тепер підраховуємо, скільки потрібно визначень (n) для одержання відносної помилки в 1%. Для таких умов розрахуємо значення :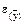

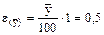
При цьому розрахункове значення t(a, f) визначаємо з формули (6.7).

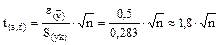
Потрібно підібрати таку кількість дослідів (п), щоб дотримувалася умова t_{(a,f) р} (розрахункове) > t_(a,f)т (табличного).

Якщо провести три досліди, то f = п – 1 = 3 - 1 = 2, для а = 0,95 і f = 2t_(a,f) = 4,30.

Для цих умов t_(a,f)р =1,8 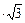=1,8·1,73 = 3,12.

Умова t_р > t_T не виконується, отже потрібно збільшити кількість дослідів.

Якщо провести 4 досліди, то f = n – 1 = 4 - 1 = 3, для а = 0,95 і f = 3·t_(a,f) = 3,18; для цієї умови

t_(a,f)р = 1,8 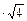= 3,6

Умова t_р > t_T дотримується, отже, кількість дослідів n = 4 забезпечує точність середнього визначення в 1 % із довірчою ймовірністю а = 0,95.