Різноманітні засоби рішення задачі оптимізації

Геометрично розв'язання задачі оптимізації полягає в досягненні найвищої точки поверхні відгуку, що відповідає перебуванню максимуму функції y = f (х₁ х₂, х₃, ...х_n) багатьох змінних.

У випадку, якщо вигляд цієї функції відомий, що рівнозначно знанню про механізм процесу, що оптимізується, максимум функції може бути визначений аналітичним шляхом без проведення додаткового експерименту. Проте, при оптимізації технологічних процесів, дослідник змушений розв'язувати задачу оптимізації експериментально. Шлях розв'язання такої задачі можна уявити як маршрут, по якому рухається дослідник із деякої вихідної точки в область максимуму. Існує декілька методів екстремального пошуку, найбільш поширений у різних технологічних дослідженнях є метод Зайделя-Гауса. Метод Зайделя-Гауса передбачає послідовне варіювання обраних факторів у міру знаходження приватних максимумів кожного з них.

Прямування до екстремуму при використанні цього методу для двофакторного експерименту наведено на рисунку 6.2.

Таким чином, багаторазово варіюючи кожний фактор при фіксованому положенні іншого, досягають оптимальної області. Проте оптимізація за Зайделем-Гаусом має ряд недоліків:

- довгий шлях до оптимуму;

- громіздка система рівнянь, що подає результати дослідів в аналітичній формі;

- принципова неможливість з’ясовування взаємодії факторів, що може мати велике значення в технологічних процесах.

Дослідження з застосуванням математичних методів планування (метод випадкового балансу, факторний експеримент, метод Бокса-Уілсона) успішно використовуються для оптимізації різноманітних технологічних процесів. Основною перевагою методів математичного планування порівняно з класичними методами дослідження є можливість одночасного вивчення великої кількості факторів, що діють у системі. При цьому враховується взаємодія факторів і є можливість оцінити її ефекти.

При оптимізації багатофакторних систем з істотними міжфакторними взаємодіями першим кроком повинен бути добір суттєвих факторів. Це може бути вирішено шляхом плануванням експерименту методом випадкового балансу. Для знаходження найкращої комбінації відібраних суттєвих факторів є ефективним метод крутого сходження (метод Бокса-Уілсона), який являє собою факторний експеримент із наступним рухом по градієнту.

Перевагами досліджень із застосуванням математичних методів є скорочення часу та витрат і велика ймовірність досягнення дійсного оптимуму.

Для пошуку оптимуму використовують скорочену схему дослідження. Це можливо тільки в тому випадку, якщо відносно поверхні відгуку до початку експерименту (апріорі) прийняти певні припущення, головними з яких є неперервність поверхні відгуку і наявність тільки одного екстремуму.

Якщо знати значення параметрів оптимізації в декількох сусідніх точках факторного простору, то можна уявити результати, що очікуються в інших сусідніх точках. Отже, можна знайти такі точки, для яких очікується найбільше збільшення (або зменшення, якщо шукаємо мінімум) параметра оптимізації. Такий експеримент треба переносити саме в ці точки. При цьому слід просуватися в потрібному напрямку. Зробивши новий експеримент, знову оцінюють напрямок, у якому варто рухатися. У силу єдності максимуму ми його, нарешті, досягнемо. Такий принцип знаходження оптимуму називається кроковим. Експериментальне дослідження із застосуванням математичних методів планування проводиться у певному порядку, що ілюструє рисунок 6.2:

а) досліджується якесь сходження, тобто частина поверхні відгуку, для чого проводиться серія дослідів для одержання опису поверхні відгуку біля вихідної точки експерименту — А.

б) за знайденими коефіцієнтами регресії визначається напрямок прямування у бік найбільш різкої зміни функції (до деякої точки максимуму -В).

в) в області точки максимуму В проводиться нова серія дослідів, за результатами якої з’ясовується, чи є точка В екстремумом. У разі потреби аналогічно здійснюється прямування у бік збільшення результату процесу до точки С, що відповідає новому максимуму.

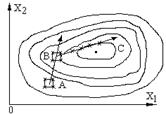
Рисунок 6.2 - Схема прямування до максимуму

по методу крутого сходження

Більшість математичних методів планування екстремальних експериментів дає можливість за результатами експериментів скласти математичний опис процесу у вигляді рівняння регресії. У цьому випадку планування експерименту і його проведення складаються з таких етапів:

а) висловлюється гіпотеза про можливість опису процесу рівнянням регресії (степеневим рядом визначеного порядку);

б) відповідно до цієї гіпотези планується і проводиться експеримент;

в) за результатами експерименту розраховуються коефіцієнти регресії і складається математичний опис відповідно до початкової гіпотези;

г) проводиться статистична оцінка значущості коефіцієнтів рівняння регресії;

д) здійснюється статистичний аналіз адекватності (відповідності) отриманого рівняння дійсному протіканню процесу, перевіряється початкова гіпотеза, а також гіпотези, що сприяють максимальному спрощенню рівняння при збереженні його адекватності досліджуваному процессу;

е) використовуючи отримане рівняння, тим чи іншим методом вирішується питання про визначення оптимальних умов протікання досліджуваного процесу.