Поняття стійкості. Дослідження і аналіз стійкості за коренями характеристичного рівняння.

Одним з основних показників, що характеризують САК, є стійкість.

Автоматична система є стійкою, якщо вона повертається до усталеного режиму після припинення дії збурення, яке вивело її з цього стану.

Нестійка система не повертається до стану рівноваги, з якого вона вийшла з тих або інших причин. Вихідна величина такої системи безперервно збільшується або здійснює недопустимо великі коливання. Звичайно нестійкі автоматичні системи непридатні для практичного використання.

Російський вчений О.М.Ляпунов запропонував оцінювати стійкість системи на основі аналізу рівняння динаміки, що описує систему. Вільний рух лінійної динамічної системи описується однорідним диференціальним рівнянням із сталими коефіцієнтами та без правої частини такого виду:

,

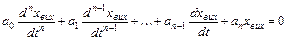де 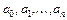– сталі коефіцієнти, що визначаються параметрами системи (сталими часу, коефіцієнтами підсилення).

В операторній формі це рівняння переписується так:

,

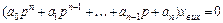звідки можна одержати характеристичне рівняння

.

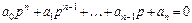Розв’язання цього рівняння дає корені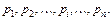

Як відомо з курсу математики, розв’язання вихідного диференціального рівняння, що описує автоматичну систему, являє собою суму експонент, показники степенів яких дорівнюють добутку коренів характеристичного рівняння р_і на час t:

,

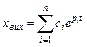де с_і – сталі інтегрування, що визначаються з початкових умов.

За означенням система є стійкою, якщо вихідна величина прямує до нуля при збільшенні часу, а це можливо тільки тоді, коли всі складові (експоненти) з часом прямуватимуть до нуля.

Оскільки всі коефіцієнти с_і є величини сталі, то кожна складова залежить тільки від р_і. Так, якщо р_і додатне дійсне число, то з часом зростає до нескінченності, бо 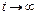; якщо р_і – від’ємне дійсне число, з часом прямує до нуля. Нарешті, якщо р_і комплексне число, яке дорівнює 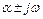, то:

.

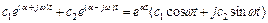Рівняння описує коливальний процес, амплітуда якого зростає або зменшується залежно від знака дійсної частини 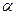комплексного кореня р. Якщо дійсна частина кореня додатна, матимемо коливальний процес з амплітудою, що зростає з часом; якщо ж дійсна частина кореня від’ємна, то амплітуда коливань з часом прямує до нуля.

Приклад.

Зробити висновок про стійкість САК, що описується рівнянням

.

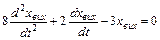Характеристичне рівняння системи: 8р² + 2р – 3=0.

Розв’язавши це рівняння знайдемо його корен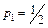і:

і .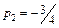

Загальний розв’язок рівняння має такий вигляд:

,

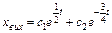звідки випливає, що вихідна величина змінюється по кривій, яка є сумою двох експонент. Причому перша експонента наростає (р>0), а друга – зменшується (р<0). В кінцевому підсумку крива 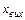буде наростати до нескінченності. Отже, задана САК буде нестійкою.

На підставі сказаного можна сформулювати умову стійкості лінійних систем керування. Щоб САК, яка описується лінійним диференціальним рівнянням із сталими коефіцієнтами, була стійкою, необхідно й достатньо, щоб дійсні корені характеристичного рівняння, яке відповідає цьому диференціальному рівнянню, були від’ємними, а комплексні корені мали від’ємну дійсну частину.

Отже, дослідження стійкості системи зводиться до визначення знаків дійсних частин коренів характеристичного рівняння. Якщо зобразити корені характеристичного рівняння у вигляді точок на комплексній площині, для стійкості системи необхідно, щоб усі корені лежали зліва від уявної осі.

Недоліком аналізу стійкості за виглядом коренів характеристичного рівняння є відомі складнощі при аналітичних методах розв’язання алгебраїчних рівнянь високого порядку, які при n > 4 не мають загального розв’язку. Тому було розроблено методи, що дозволяють досліджувати САК без знаходження коренів характеристичного рівняння, які дістали назву критеріїв стійкості. Існують два основних види критеріїв стійкості: алгебраїчні і частотні. До алгебраїчних критеріїв стійкості належать критерії Рауса, Гурвіца, Вишнєградського, Льєнара-Шіпара, до частотних – критерій Михайлова та його наслідок, критерій Найквіста, метод D-розбиття, логарифмічні критерії.