Загальні відомості про частотні характеристики

Для аналізу динаміки автоматичних систем і їх ланок широко застосовують частотні методи, при яких передбачається дія на систему (ланку) змінного сигналу за синусоїдальним законом. Якщо система (ланка) лінійна, то при подачі на вхід синусоїдального сигналу з амплітудою А_вх і частотою ω на виході також буде синусоїдальний сигнал з такою самою частотою і амплітудою А_вих, але максимум вихідного сигналу буде зсунутий на кут φ від максимуму вхідного сигналу, тобто якщо

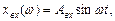то

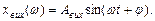
Рис.4.2. Графік гармонічних коливань

вхідної і вихідної величин

У показниковій (комплексній) формі вхідні й вихідні сигнали записують так:

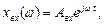
де е – основа натурального логарифма;

φ – кут зсуву між вхідною і вихідною величинами;

Якщо поділити вихідну величину на вхідну, дістанемо частотну передаточну функцію:

Слід зауважити, що вихідна величина і кут зсуву залежать від частоти синусоїдальної дії.

Частотну передаточну функцію легко одержати з передаточної функції в операторній формі, замінивши оператор р на jω.

Наприклад, якщо є передаточна функція 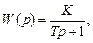то частотна передаточна функція 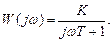Помножимо чисельник і знаменник на спряжену із знаменником комплексну величину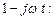

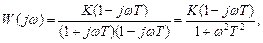
де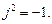

Відділивши дійсну і уявну частини, отримаємо:

У комплексній передаточній функції є дійсна і уявна частини:

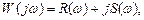
де ; .

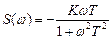Модуль частотної передаточної функції

Кут зсуву можна визначити з виразу

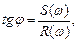або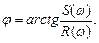

Стосовно до взятого прикладу

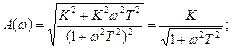
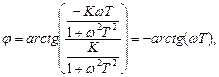
звідки

Як видно з виразів для модуля і фази частотної передаточної функції, вони залежать від частоти гармонічного сигналу ω.

Графік залежності модуля частотної передаточної функції від частоти називається амплітудно-частотною характеристикою (АЧХ).

Залежність кута зсуву від частоти називають фазочастотною характеристикою (ФЧХ).

Ці дві характеристики будують у прямокутних (декартових) координатах, на осі абсцис яких відкладають частоту, а на осі ординат – модуль передаточної функції або кут зсуву.

Залежність передаточної функції від частоти будують у комплексній площині (рис.4.3). Ця характеристика називається амплітудно-фазовою характеристикою (АФХ), або годографом передаточної функції.

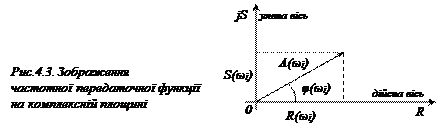Всі частотні характеристики можуть бути побудовані в логарифмічному масштабі. У цьому випадку їх називають логарифмічними частотними характеристиками.