за допомогою формули Мейсона.

Формула Мейсона використовується для спрощення графа, та знаходження передаточної функції замкнутої системи автоматичного керування по відомому графу системи.

Формулу записують у вигляді:

,

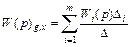де g – вхідна, а х – вихідна величини системи (графа); 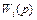– передаточна функція і-го простого шляху від вершини g до вершини х, що дорівнює добутку передаточних функцій дуг, які належать цьому шляху (контуру);
m – кількість таких шляхів (для спрощення запису передаточних функцій далі не писатимемо знак оператора р); 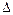– визначник графа.

Визначник графа записується у вигляді:

,

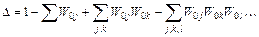де 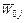– передаточна функція j-го простого контуру, яка дорівнює добутку передаточних функцій всіх дуг даного контуру.

Перша складова 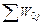є сумою всіх подібних простих контурів.

Друга складова 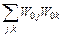– сума пар контурів j та k, що не доторкуються до інших контурів ( 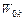– результуюча передаточна функція контуру k, подібна до ).

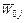Третя складова формули детермінанта 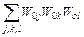– сума добутків передаточних функцій відповідних контурів, що не доторкуються. Аналогічно можна обчислювати й інші складові, якщо вони є в даному складному графі. При цьому треба мати на увазі, що недоторкуючими називають такі два контури, які не мають спільних дуг або вершин. Трійка, четвірка і т.д. контурів вважається недоторкуючою, якщо будь-яка пара контурів цієї трійки, четвірки і т.д. в свою чергу будуть недоторкуючими.

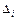– детермінант підграфа, який можна дістати з головного (вихідного) графа при виключенні дуг та вершин і-го простого шляху, а також дуг та вершин, інцидентних цим вершинам.

Запишемо передаточну функцію системи автоматичного керування за завданням g згідно з формулою Мейсона відповідно до рис.8.1 (при цьому вважатимемо f=0). З рис.8.1,в видно, що від вершини g до вершини х є два
(І і ІІ) простих шляхи з такими передаточними функціями:

;

.

Крім цього, у вихідному графі є три контури (позначимо їх 1,2,3), передаточні функції яких мають вигляд:

;

;

.

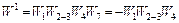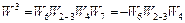Недоторкуючих пар і контурів граф не має, тому його визначник матиме вигляд:

.

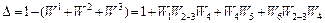Підграфи, які відповідають простим шляхам від вершини g до х, замкнутих контурів не мають, тому

.

Формула Мейсона в цьому разі матиме вигляд:

.

Якщо потрібно знайти передаточну функцію за збуренням, то враховують, що g=0. При цьому від вершини f до х маємо лише один простий шлях 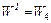. Відповідний підграф у цьому разі не має замкнутих контурів і його визначник дорівнює одиниці: .

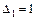Передаточна функція за Мейсоном матиме вигляд:

.

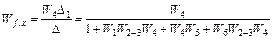Література

1. Валюх О.А., Максимів В.М. Елементи теорії автоматичного керування. Лінійні системи неперервної дії: – Львів. Афіша, 2002. –124 с.

2. Головко Д.Б. та ін. Автоматика і автоматизація технологічних процесів: Підручник. – К.: Либідь, 1997. – 232 с.

3. Мартиненко И.И. Основы автоматики: Учеб. пособие для с.-х. техникумов. – Киев: Вища школа. Голов. изд-во, 1980. – Яз.укр. – 168 с.

4. Попович М.Г., Ковальчук О.В. Теорія автоматичного керування: Підручник. – К.: Либідь, 1997. – 554 с.

5. Силин Р.И., Стадник Я.Ф., Третьяков В.В. Основы автоматики и автоматизации производственных процессов. Сборник задач. – Львов: Вища школа. Изд-во при Львов. ун-те, 1985. – 120 с.

6. Терган В.С. и др. Основы автоматизации производства: учеб. пособие для машиностроительных спец. – М.: машиностроение, 1982. 269 с., ил.

7. Чекваскин А.Н. и др. Основы автоматики: Учеб. пособие для техникумов. – М.: Энергия, 1977. – 448 с.

Конспект лекцій

для студентів спеціальності 6.090200

“Обладнання лісового комплексу”

денної та заочної форм навчання

Р.Я. Джигалюк

Комп’ютерний набір та верстка: Р.Я.Джигалюк.

Редактор: Л.Ю. Тиха.

Підписано до друку. Формат 60х84/16. Папір офс.

Гарн. Таймс. Ум. Друк. Арк. 1,5. Обл.-вид. арк. 1,0.

Тираж 50 прим. Зам. 3697.

Редакційно-видавничий відділ

Луцького державного технічного університету

43018 м.Луцьк, вул.Львівська, 75.

Друк – РВВ ЛНТУ.