Правила перетворення структурних схем
Знаючи правила перетворення структурних схем, можна досить просто розв’язати завдання перетворення одноконтурних і деяких багатоконтурних систем.
При цьому, під одноконтурною замкнутою системою розуміють систему, при розмиканні якої в довільній точці можна дістати ланцюжок ланок, в якому відсутні паралельно з’єднані ланки і ланки, охоплені зворотними зв’язками. Багатоконтурною називають систему, яка має в своєму складі паралельно з’єднані ланки, а також ланки з місцевими зворотними зв’язками.
Найпростіші перетворення структурних схем та їх окремих елементів було розглянуто раніше.
При послідовному з’єднання ланок результуюча передаточна функція W(p) ланок у загальному вигляді може бути визначена як добуток передаточних функцій Wі(p) ланок:
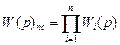 ,
,
а при паралельному – як їх сума:
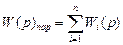 .
.
Передаточна функція ланки із зворотним зв’язком (групи ланок, що охоплені зворотним зв’язком матиме вигляд:
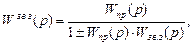
де знак “плюс” відповідає від’ємному, а знак “мінус” – додатному зворотному зв’язку; 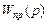 – передаточна функція прямого каналу, що є передаточною функцією окремої ланки або послідовно з’єднаних ланок, що охоплюються зворотним зв’язком;
– передаточна функція прямого каналу, що є передаточною функцією окремої ланки або послідовно з’єднаних ланок, що охоплюються зворотним зв’язком; 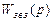 – передаточна функція самої ланки зворотного зв’язку (рис.5.2).
– передаточна функція самої ланки зворотного зв’язку (рис.5.2).
 |
Якщо передаточна функція зворотного зв’язку 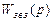 дорівнює одиниці, то такий зворотний зв’язок називають одиничним (рис.5.3) і передаточна функція ланки в такому випадку має вигляд:
дорівнює одиниці, то такий зворотний зв’язок називають одиничним (рис.5.3) і передаточна функція ланки в такому випадку має вигляд:
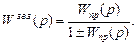
Розглянемо можливості перетворення структурної схеми, наведеної на рис.5.4. Ця схема є багатоконтурною (об’єктом є ланка W4(p)) і має в своєму складі ланки з додатними зворотними зв’язками, кожний з яких охоплює по дві ланки. Одна з них входить також до контура іншого зворотного зв’язку. Такі структурні схеми мають назву схем з перехресними зворотними зв’язками. Їх не можна перетворити за допомогою розглянутих вище формул. Тому ці схеми треба перетворити таким чином, щоб ліквідувати зв’язки, що перехрещуються.
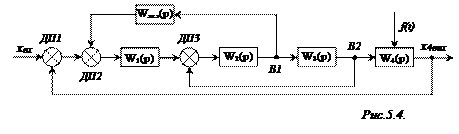
Для перетворення структурних схем із перехресними зворотними зв’язками використовуються правила переносу додатних пристроїв (на схемі ДП1, ДП2, ДП3) та вузлів (позначених В1, В2).
Загальний принцип переносу додатного пристрою або вузла в схемі полягає в тому, що при ліквідації явища перехрещування зворотних зв’язків вихідні величини ланок повинні бути незмінними. Цей принцип добре ілюструють схеми переносу додатного пристрою ДП (рис.5.5, а, б, в) і
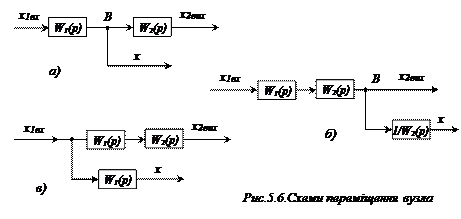
вузла В (рис.5.6, а, б, в).
На рис.5.5, б показано перенос ДП вправо по ходу процесу. При цьому величина х не проходитиме через ланку W2(p), що має місце у вихідній схемі. Для того, щоб процес у перетвореній схемі не змінився, необхідно ввести додаткову ланку W2(p) між точкою вводу сигналу х і ДП.

Якщо ДП переміщується вліво (проти ходу процесу), то між точкою прикладання величини х і ДП потрібно ввести ланку, передаточна функція якої буде оберненою функцією ланки, через яку ДП переміщується вліво.
На рис.5.6. показано вихідну (а) і перетворені (б,в) схеми переміщення вузла В вліво та вправо відносно початкового положення. При цьому, при переміщенні вузла також необхідно ввести додаткові ланки. Якщо вузол В переміщується вправо, то для того, щоб величина х не змінилася, необхідно ввести в ланцюг х ланку з передаточною функцією, оберненою передаточній функції, через яку було переміщено вузол В. Якщо вузол В переміщується вліво, треба ввести додаткову ланку з передаточною функцією, що дорівнює передаточній функції ланки, через яку переміщується вузол В.
Повертаючись до схеми на рис.5.4, покажемо, що для ліквідації перехресних зворотних зв’язків можна перемістити додатний пристрій ДП2 вправо, об’єднавши його з ДП3, або вузол В1 вправо, об’єднавши його з вузлом В2.
Перетворена схема з переносом вузла В1 вправо показана на рис.5.7, а перетворена схема з переносом ДП2 вправо і об’єднання його з ДП3 – на рис.5.8.

Перехрещування зворотних зв’язків можна ліквідувати також переміщенням вузла В2 вліво і об’єднанням його з вузлом В1. В цьому випадку в ланцюг одиничного зворотного зв’язку треба ввести додаткову ланку з передаточною функцією W3(p).
Ліквідувавши перехрещення зворотних зв’язків, неважко провести спрощення одержаних структурних схем за раніше викладеними правилами і наведеними формулами.
Дата добавления: 2016-03-27; просмотров: 1479;
