Алгебраїчний критерій стійкості Гурвіца.
Цей критерій стійкості запропонований швейцарським математиком Гурвіцем у 1895 році. Він формулюється так. Якщо система описується характеристичним рівнянням виду
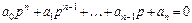 ,
,
то для стійкості САК необхідно й достатньо, щоб при коефіцієнті 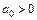 всі діагональні мінори визначника системи, складеного з коренів рівняння
всі діагональні мінори визначника системи, складеного з коренів рівняння
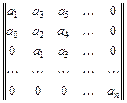 ,
,
були більші від нуля.
Тут по головній діагоналі визначника виписані всі коефіцієнти від а1 до аn у порядку зростання індексів. Вгору від елементів діагоналі стовпчики доповнені коефіцієнтами із зростаючими індексами, а вниз – із спадними індексами. На місцях коефіцієнтів, індекси яких більші за n і менші від нуля, поставлено нулі.
Діагональні мінори визначають із головного детермінанта Гурвіца викреслюванням відповідних стовпчиків і рядків. За означенням критерію стійкості Гурвіца, запишемо:
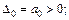
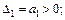
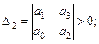
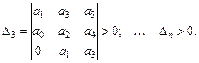
Як приклад дослідимо стійкість за Гурвіцем системи, що описується характеристичним рівнянням четвертого порядку:
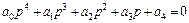 ,
,
де 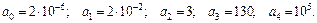
Складемо визначник Гурвіца
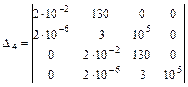 ;
;
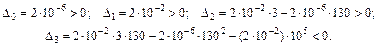
Оскільки третій діагональний мінор 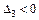 , то, не обчислюючи четвертого діагонального мінора
, то, не обчислюючи четвертого діагонального мінора 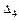 , можна сказати, що задана САК буде нестійкою в роботі.
, можна сказати, що задана САК буде нестійкою в роботі.
Слід зазначити, що критерій Гурвіца практично прийнятий для дослідження стійкості САК, що описуються диференціальними рівняннями порівняно невисоких порядків (до п’ятого порядку). Для рівнянь вищого порядку використання цього критерію ускладнюється, бо умова стійкості виражається громіздким визначником, складеним з коефіцієнтів рівняння, і важко знаходити числові значення діагональних мінорів.
Дата добавления: 2016-03-27; просмотров: 953;
