Особливі крітерії стійкості кріптосистем
Існують два основних класа стійкості кріптосистем:
Ідеально (безумовно) стійкі, або досконалі системи, для яких стійкість кріптоаналізу (дешифрування) без знання ключа не залежить від розрахункової потужності опонента. Ми будемо називати їх теоретично недешифруємими.
Розрахунково стійкі системи, у якіх стійкість кріптоаналізу залежить від розрахункової потужності опонента.
Система є теоретично недешифруємою, якщо будь-яка криптограма 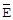 , отримана у ній, при відсутності знання про ключ
, отримана у ній, при відсутності знання про ключ 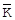 , не містить ніяких відомостей про повідомлення
, не містить ніяких відомостей про повідомлення 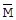 , зашифроване у цю кріптограму. У відповідності з терією інформації це має місце, коли (при відсутності відомостей про ключ) дорівнює нулю взаємна інформація між численністю повідомлень М та численністю кріптограм Е, тобто І(Е, М) =0, де І(Е, М) =Н(М) - Н(М/Е), Н(м) - ентропія джерела повідомлень, Н(М/Е) - умовна ентропія численності повідомлень М при заданій численності криптограм Е.
, зашифроване у цю кріптограму. У відповідності з терією інформації це має місце, коли (при відсутності відомостей про ключ) дорівнює нулю взаємна інформація між численністю повідомлень М та численністю кріптограм Е, тобто І(Е, М) =0, де І(Е, М) =Н(М) - Н(М/Е), Н(м) - ентропія джерела повідомлень, Н(М/Е) - умовна ентропія численності повідомлень М при заданій численності криптограм Е.
При ідеальному шифруванні фактично виникає "обрив канала" від легальних користувачів до опонентів.
Равносильне визначення ідеального шифрування встановлює незалежність будь-якої пари 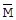 та
та 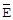 від численності повідомлень та численності кріптограм, тобто тоді, коли умовна ймовірність передачі визначеного повідомлення при отриманні визначеної криптограми залишається завжди рівною апріорній ймовірності передачі цього повідомлення.
від численності повідомлень та численності кріптограм, тобто тоді, коли умовна ймовірність передачі визначеного повідомлення при отриманні визначеної криптограми залишається завжди рівною апріорній ймовірності передачі цього повідомлення.
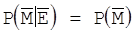 (2.4)
(2.4)
З визначення ТНДШ видно, що найкращій засіб кріптоаналізу для такої системи при невідомому ключі дешифрування складається в ігноруванні кріптограми та в випадковому угадуванні повідомлень по відомій апріорно ймовірності.
Розглянемо приклад побудови теоретично недешифруємих систем (див. мал.2.2).
Припустимо, що повідомлення є двоїчною послідовністю 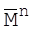 довжини n. Тоді можна формувати кріптограму як двоїчну послідовність такої ж довжини n за наступним правилом:
довжини n. Тоді можна формувати кріптограму як двоїчну послідовність такої ж довжини n за наступним правилом:
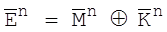 (2.5)
(2.5)
використовуючи побітне додавання Å з ключем 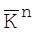 , який також є двоїчною послідовністю довжини n.
, який також є двоїчною послідовністю довжини n.
Наприклад,
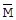 011001101111010001110
011001101111010001110
Å
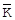 010011110101100110101
010011110101100110101
___________________________
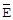 001010011010110111011
001010011010110111011
При відомому ключі 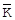 , який повинен бути переданий на сторону прийому будь-яким секретним чином, повідомлення легко відновлюється по тій же формулі, по якій проводилося шифрування
, який повинен бути переданий на сторону прийому будь-яким секретним чином, повідомлення легко відновлюється по тій же формулі, по якій проводилося шифрування
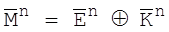 (2.6)
(2.6)
Покажемо, що якщо двоїчні елементи ключа вибираються взіємнонезалежними та равноймовірними, то цього достатньо, щоб описана вище система була ТНДШ.
Елементи ключа вибирають незалежно, тому достатньо довести рівність Р(М|Е) =Р(М) для одного елемента. По формулі Бейеса
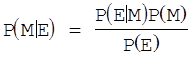 (2.7)
(2.7)
Із графа, який представлено на мал.2.3. і який показує можливості шифрування при рівноймовірних символах ключа слідчить, що 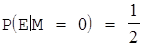 ,
, 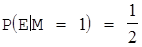 .
.
Звідси р(Е) =р(М=0) р(Е|М=0) +р(М=1) р(Е|М=1) =0.5(р(М=0) +р(М=1)) = 0.5 і отимаємо
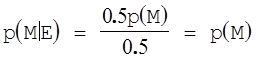 (2.8)
(2.8)
Останнє рівняння і є умовою теоретичної недешифруємості.
Відзначимо, що дана система має суттєвий недолік, який полягає у тому, що потрібна довжина ключа N повинна дорівнювати довжині повідомлення, тому необхідна генерація, передача у секреті, зберігання великого числа біт ключа, що робить розглядаєму систему дорогою та непридатною для масового використання, доступною лише для привілейованих користувачів. Але поки на доведено, що умова n=N є необхідною для побудови ТНДШ.
Доведемо: необхідна умова ТНДШ складається з того, що число можливих кодів, використовуємих у ТНДШ повинно бути не менш, ніж число повідомлень, які засекречуються на цих ключах. Дійсно, нехай є L можливих повідомлень 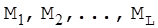 . Виберемо фіксований ключ
. Виберемо фіксований ключ 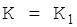 . При одному й тому ж ключі різні повідомлення переходять у різні кріптограми з ймовірністю
. При одному й тому ж ключі різні повідомлення переходять у різні кріптограми з ймовірністю 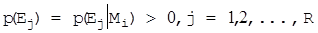 (граф такої системи
(граф такої системи
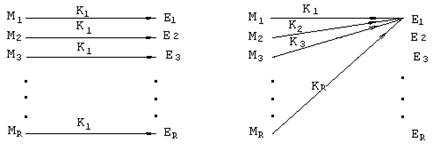 |
шифрування - на мал.2.5.
| Мал.2.5. Граф шифрування одним ключом. | Мал.2.6. Граф шифрування в одну криптограму. |
Оскільки передбачається, що система є ідеальною, то по визначенню для будь-якого повідомлення 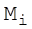 та кріптограми
та кріптограми 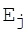 повинна виконуватися умова:
повинна виконуватися умова: 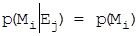 , з якого, враховуючи, що
, з якого, враховуючи, що
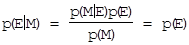 (2.9)
(2.9)
і виходить, що 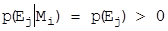 . Тоді для будь-якої обраної кріптограми (наприклад
. Тоді для будь-якої обраної кріптограми (наприклад 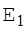 ) існують нульові ймовірності переходу у неї з будь-якого повідомлення
) існують нульові ймовірності переходу у неї з будь-якого повідомлення 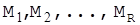 , але оскільки різні повідомлення можуть переходити в одну й ту ж саму кріптограму тільки на різних ключах, то кожному такому переходу можуть відповідати різні ключі
, але оскільки різні повідомлення можуть переходити в одну й ту ж саму кріптограму тільки на різних ключах, то кожному такому переходу можуть відповідати різні ключі 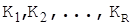 .
.
Відповідний граф для отримання кріптограми 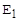 представлений на мал.2.6. Тоді ми отримаємо стільки ж ключів, скільки є повідомлень, тобто R.
представлений на мал.2.6. Тоді ми отримаємо стільки ж ключів, скільки є повідомлень, тобто R.
Нехай ключ представляє собою послідовність довжиною N із алфавіта К об’ємом 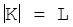 . Тоді загальне число ключів буде дорівнювати
. Тоді загальне число ключів буде дорівнювати 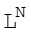 . Порівнюючи це число ключів з числом повідомлень
. Порівнюючи це число ключів з числом повідомлень 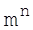 , де m - об’єм алфавіта джерела, n - довжина повідомлення, отримаємо, що необхідна умова ТНДШ приймає вигляд
, де m - об’єм алфавіта джерела, n - довжина повідомлення, отримаємо, що необхідна умова ТНДШ приймає вигляд
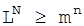 , або
, або 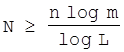 (2.10)
(2.10)
У частному випадку, коли L=m, отримаємо, що N=n, що співпадає з достатньою умовою, яку отримали вище для прикладу двоїчного кодування по модулю два.
Але нема необхідності шифрувати усі послідовності, які можна скласти із символів джерела повідомлень. У дійсності можна шифрувати тільки так звані "типічні" послідовності, які з’являються з ненульовою ймовірністю.
Із теорії інформації бачимо, що при 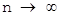 число типових послідовностей ~
число типових послідовностей ~ 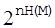 , де H(M) - ентропія джерела повідомлення. Типові послідовності приблизно рівноймовірні, їх сумарна ймовірність збігається до одиниці. На підставі раніше доведеного твердження, шифруючи тільки типові послідовності, отримаємо необхідну умову ТНДШ:
, де H(M) - ентропія джерела повідомлення. Типові послідовності приблизно рівноймовірні, їх сумарна ймовірність збігається до одиниці. На підставі раніше доведеного твердження, шифруючи тільки типові послідовності, отримаємо необхідну умову ТНДШ:
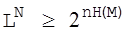 , або
, або 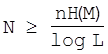 (2.11)
(2.11)
Оскільки для будь-яких джерел Н(М) <logm, то (7) дає меньш жорсткі умови, ніж (6). Чим більше надлишок джерела, тим менше його ентропія. Таким чином для забезпечення найбільш економного з точки зору ключа ідеального шифра, необхідно попередньо стиснути повідомлення, а потім провести додавання по модулю два з ключовою послідовністю.
Таким чином, необхідною умовою ТНДШ є пропорційність довжини ключа довжині послідовності. Тільки коефіцієнт цієї пропорційності для надлишкових джерел може бути декілька зменшений в порівнянні з одиницею.
Приклад: нехай задані такі параметри джерела повідомлень та ключа: L=2, m=32, ентропія джерела Н(М) =0.5 біта на букву. Тоді при шифруванні усіх послідовностей джерела довжина ключа повинна бути N=5n, тоді як після стиснення повідомлення такого джерела вони можуть бути зменшені вдвічи.
Дата добавления: 2016-02-24; просмотров: 752;
