Вычислительно стойкие криптосистемы
Криптосистема называется вычислительно стойкой, если наилучший алгоритм дешифрования требует времени (или оборудования) больше, чем имеется в распоряжении оппонента.
В частности может оказаться, что требуемое время криптоанализа превышает то время в течение которого рассматриваемое сообщение перестает быть актуальным, либо получение даже правильного сообщения не окупает затрат затраченных на процедуру криптоанализа.
Существенная сложность при разработке вычислительно стойких криптосистем возникает в связи с определением наилучшего алгоритма криптоанализа. В действительности эта задача не решена ни для одной мощной криптосистемы, т.е. для достаточно мощных шифров наилучшие такие алгоритмы просто не известны. Поэтому можно говорить лишь об известных в настоящее время наилучших методах криптоанализа, которые применимы к отдельным классам шифров или разработаны для конкретных шифров. (Обычно ограничиваются наилучшими известными в настоящее время алгоритмами криптоанализа и берут значительный запас на быстродействие и количество вычислительных средств) Поэтому теоретически всегда существует возможность, что будет найден некоторый новый метод криптоанализа, который позволит решить задачу "в реальном времени". Однако для современных шифров вероятность такого "прорыва" весьма мала, поскольку он требует решения весьма сложных, и обычно давно известных в математике задач. Это особенно верно для систем с открытым ключом, для которых задача криптоанализа может быть четко сформулирована как некоторая вполне конкретная математическая задача.
В современной математике существует область "Теория сложности алгоритмов", где различают "простые" и "сложные" задачи. Задачи полиномиальной сложности, для решения которых необходимое число элементарных операций является полиномиальной функцией от размерности задачи, относятся к простым. Время T(N) для их решения ~ N n, где N - размерность задачи. Наиболее сложные (трудные) задачи требуют для своего решения числа операций, которое экспоненциально зависит от размерности задачи, т.е. T(N) ~ abN, где aиb>0 некоторые постоянные, в силу чего весь класс таких задач называется EXPTIME.
Нужно избегать построения криптосистем с полиномиальным временем криптоанализа и стараться строить криптосистемы так, чтобы их вскрытие относилось к задачам второго класса сложности.
 |
Помимо двух уже рассмотренных классов задач в теории сложности выделяют еще один важный класс задач, называемых недетерминистско - полиномиальными (NP задачами). NP - задачи - это задачи, для которых пока неизвестны алгоритмы решения с полиномиальной сложностью (это не означает, что они вообще не существуют). Однако, если решение такой задачи найдено, то проверка его правильности это задача полиномиальной сложности.
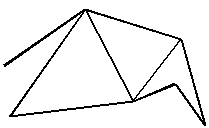
Рис.2.8. Граф для поиска Гамильтонова цикла
Имеется достаточно широкий класс известных NP-задач, имеющий многовековую историю попыток их полиномиального решения. Так, например, для заданного графа (см. рис 2.8) нужно найти путь (Гамильтонов путь) проходящий по всем вершинам графа только один раз. Не известен алгоритм нахождения Гамильтонова цикла полиномиальной сложности от числа вершин графа. Хотя, если такой цикл найден, то проверить правильность предлагаемого решения всегда можно с помощью алгоритма полиномиальной сложности.
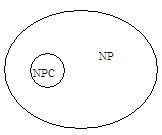 |
Среди задач NP класса имеется подкласс (см. рис.2.9) наиболее сложных задач, которые называются NP - трудными. Это задачи, обладающие следующим свойством: если для какой - то из них найдется алгоритм решения с полиномиальной сложностью, то это будет означать, что существуют алгоритмы с полиномиальной сложностью для решения всех задач из NP класса.
Рис.2.9. Соотношение между задачами NP и NPC класса.
Таким образом, нужно стремиться строить такие криптографические системы, чтобы их криптоанализ при неизвестном ключе был бы эквивалентен решению NP трудной задачи, для которой существование полиномиального алгоритма означает существование полиномиального алгоритма для решения всех задач из NP класса (что, учитывая огромный список таких задач очень маловероятно).
Отметим, однако, что имеется важное, существенное отличие в подходе к оценке сложности произвольных алгоритмов и сложности криптоанализа. В классической теории сложности оценка производится для самой трудной задачи, т.е. при наихудших входных данных, тогда как во втором - при всех входных данных, в том числе и при наилучших, т.е. при наиболее благоприятных для криптоанализа ключах.
Помимо рассмотренных ранее классов детерминированных алгоритмов, существует еще класс так называемых рандомизированных полиномиальных алгоритмов. К нему принадлежат такие алгоритмы, которые имеют полиномиальную сложность, но дают правильный ответ на поставленную задачу лишь с некоторой вероятностью. Очевидно, что если эта вероятность близка к единице, то с практической точки зрения, рандомизированные алгоритмы не хуже детерминированных.
Поэтому необходимо также исключить такие криптографические схемы, которые имеют рандомизированный алгоритм криптоанализа с полиномиальной сложностью.
Таким образом, основные очевидные требования к вычислительно стойким криптосистемам можно сформулировать в следующем виде:
Число ключей LN должно быть непереборно большим, например при L = 2 нужно иметь N = 64, N = 128 и т.п., поскольку в противном случае, приняв криптограмму длиною больше расстояния единственности (n > nре) можно правильно дешифровать переданное сообщение путем полного перебора ключей.
Недопустимо использование какого - либо метода шифрования, который имел бы известный поліноміально сложный от длины ключа метод криптоанализа. Желательно, чтобы сложность была экспоненциальной. Тогда, увеличивая длину ключа всегда можно обеспечить невозможность дешифровки в реальном времени. В частности, из этого следует, что криптоанализ не должен сводить
 |
Зазначимо, що хоча висновок для величини відстані єдиності був приблизним, практичний досвід свідчить, що відстань єдиності має величину того ж порядку, що дає формула Шеннона.
Дата добавления: 2016-02-24; просмотров: 1362;
