Асимметрические (открытые) криптосистемы

Криптографические системы с открытыми ключами шифрования позволяют пользователям осуществлять безопасную передачу данных по незащищенному каналу без какой-либо предварительной подготовки. Такие криптосистемы должны быть асимметрическими в том смысле, что отправитель и получатель имеют различные ключи, причем ни один из них не может быть выведен из другого с помощью вычислений.

В этих системах фазы шифрования и дешифрования отделены, и защита сообщения обеспечивается без засекречивания ключа шифрования, поскольку он не используется при дешифровании. Поэтому ключ публикуется вместе с алгоритмами шифрования и дешифрования, и это не приносит вреда защите системы. Принцип функционирования системы с открытыми ключами шифрования заключается в следующем: пользователь i шифрует сообщение М, используя открытый ключ шифрования пользователя j, и посылает шифрованное сообщение пользователю j по незащищенному каналу передачи данных. Только пользователь j может выполнить дешифрование, чтобы восстановить М, поскольку только он знает секретный ключ дешифрования. Алгоритмы шифрования Е(Encryption) и дешифрования D (Decryption) в таких системах характеризуются следующими свойствами [RIVE78]:

Свойство 1. Дешифрование шифрованного сообщения восстанавливает исходное сообщение М, т. е.

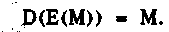
Свойство 2. Алгоритмы шифрования Е и дешифрования D являются простыми в реализации.

Свойство 3. При раскрытии алгоритма шифрования Е алгоритм дешифрования D не раскрывается, т. е. только получатель или отправитель могут дешифровать сообщение, зашифрованное алгоритмом Е, т. е. выполнить алгоритм дешифрования D.

Свойство 4. Если сообщение М сначала дешифровано, а затем зашифровано, то справедливо условие

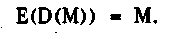
Свойство 4 не обязательно для систем с открытыми ключами, но если оно выполняется, то можно использовать цифровые сигнатуры.

Криптографические системы с открытыми ключами используют функции шифрования, обладающие свойством однонаправленности. Это свойство устанавливает условие, которое требует, чтобы защищенный ключ нельзя было восстановить по открытому ключу. Однонаправленные функции характеризуются следующими свойствами:

1. Как функция у =f(x), она вычисляется просто.

2. Имеет обратную функцию.

3. Обратную функцию крайне сложно вычислить.

Определение однонаправленной функции включает понятие сложности, которое зависит от вычислительных возможностей компьютеров. Степень сложности оценивается в затратах времени, требуемого объема памяти или произведения этих величин.

Поскольку законный получатель должен иметь возможность дешифровать сообщение, то в системах с открытыми ключами следует использовать однонаправленные функции с обходными путями, обладающие дополнительным свойством: обратная функция не должна быть вычислимой, если неизвестна специальная информация об обходных путях.

Криптографическая система RSA (Rivest-Shamir-Adleman)

Обходной путь в асимметрической схеме системы RSA основан на замене процедуры нахождения больших простых чисел процедурой их разложения на множители.

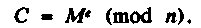
Принцип, системы RSA, можно описать следующим образом. Получатель выбирает два больших простых числа p и qтак, чтобы произведение n=pq находилось за пределами вычислительных возможностей. Исходное сообщение М может иметь произвольную длину в диапазоне 1 < М < п. Шифрованный текст С, соответствующий сообщению М, может быть получен из перестановки

Исходный текст М восстанавливается из шифрованного С обратным преобразованием

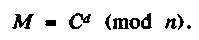
Алгоритм шифрования RSA-методом следующий:

Шаг 0: Задать входную последовательность

input

Шаг 1: Пусть 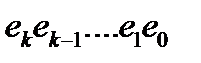- двоичное представление числа e

Шаг 2: Установить С=1

Шаг 3: Повторять шаги 3а и 3б для i=k…1,0

3а: Присвоить С значение остатка от деления С2 на n

3б: Если ei=1, то присвоить С значение остатка от деления С input на n

Шаг 4: Останов. С- шифрованный текст входа input.

Порядок дешифрирования следующий:

Получатель выбирает e и d так, чтобы выполнялись условия:

а) НОД (е, Ф(n))=1;

б) ed = 1 (mod Ф(n)) где

Ф(n) – функция Эйлера (p-1)(q-1)

НОД(a,b) – наибольший общий делитель двух чисел;

Работа схемы шифрования-дешифрования основана на теореме Эйлера, которая устанавливает, что для любого целого М, взаимно простого с n, справедливо

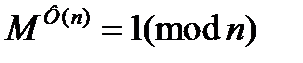
Используя условие б) получим для некоторого целого K

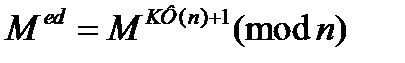
Для всех M, не делящихся на p, выполняется сравнение

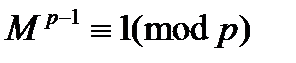
Поскольку Ф(n) кратно (p-1), справедливо

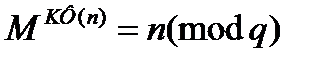
Когда 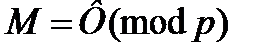, то предыдущее уравнение выполняется тривиально. По аналогии, для q справедливо

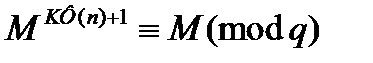
По теореме остатков для всех М справедливо

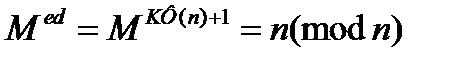
В этой системе числа е и п являются несекретными и определяют ключ шифрования. Числа d, p, и q сохраняются секретными и определяют ключ дешифрования. Если п легкоразложимо на множители р и q, то криптоаналитик найдет F(n), а затем d и раскроет систему шифрования.

Выбор показателей степени при кодировании

Выбрав простые числа р и q, а следовательно, и п, необходимо приступить к выбору показателей степени eиd. Для этого d выбирается из условия, чтобы оно было взаимно |простым с Ф(n). Это достигается вычислением остатка d(mod n) и НОД(d, Ф(и)) с помощью алгоритма Евклида. Алгоритм позволяет не только проверить, являются ли числа d и Ф(п) взаимно простыми, но также подсчитать мультипликативно - обратный к d показатель степени е. Известно, что сложность вычисления функции HОД имеет временную оценку O(log2n) [KNUT81]. На выбор показателей е к d необходимо наложить условие, чтобы эти величины превышали log2n. Если е < log2n, то малые сообщения окажутся незашифрованными.

Если будет выполняться условие 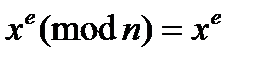, то шифр раскрывается простым перебором. Если d < log2n, то система может быть раскрыта только случайно.

Существует еще одно условие при выборе е. Как уже упоминалось, чтобы осуществить перестановки в сообщении в соответствии с функцией xе, е должно быть взаимно простым с функцией Эйлера Ф(n), или,

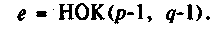
более точно, взаимно простым с НОК - наименьшим общим кратным следующих чисел:

Среди этих перестановок есть и такие, которые сохраняют сообщение, и они удовлетворяют условию конгруэнтности

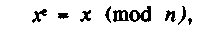
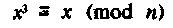
где е - нечетное число, большее 3, и n=рд. Известно, что любое решение уравнения удовлетворяет и первому уравнению. Далее отметим, что второе уравнение имеет 9 решений в диапазоне чисел 1 < х < п-1 (n=pq).

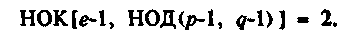
Таким образом, первое уравнение имеет по меньшей мере 9 решений. Можно показать, что уравнение конгруэнтности будет порождать ровно 9 решений, если показатель степени будет выбран из условия

Криптографический анализ RSA-системы

Вероятно, главной целью криптографического раскрытия является определение секретного показателя степени d. Известны три способа, которыми мог бы воспользоваться криптоаналитик для раскрытия величины d по открытой информации j паре (е, n).

Факторизация п

Разложение величины п на простые множители позволяем вычислить функцию Ф(n) и, следовательно, скрытое значения d, используя уравнение .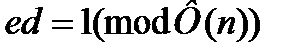

Наиболее быстрый алгоритм, известный в настоящее время
может выполнить факторизацию n за число шагов порядка

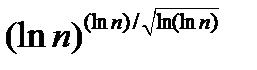
Вычисление Ф(п) без факторизации

Другой возможный способ криптоанализа связан с непосредственным вычислением функции Эйлера Ф(n) без факторизации п. В работе [RIVE78] показано, что прямое вычисление Ф(п) нисколько не проще факторизации п, поскольку Ф(п) позволяет после этого легко факторизовать п. Это можно видеть из следующего примера. Пусть

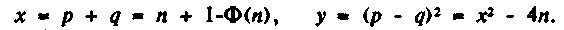
Зная Ф(n), можно определить х и, следовательно, у; зная х и у, простые р и q можно определить из следующих соотношений

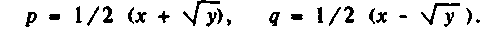
Прямая оценка d без факторизации п или вычисления Ф(n)

Третий способ криптоанализа состоит в непосредственном вычислении величины d. Аргументация этого способа основана на том, что если d выбрано достаточно большим, чтобы простой перебор был неприемлем, вычисление d не проще факторизации и если d известно, то п легко факторизуется. Это можно показать следующим образом. Если d известно, то можно вычислить величину, кратную функции Эйлера, используя условие

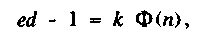
где k - произвольное целое число.

Факторизацию п можно выполнить, используя любое значение, кратное F(n). Дешифровщик, с другой стороны, может попытаться найти некоторую величину d', которая была бы эквивалентна скрытой величине d, использованной при разработке шифра. Если существует много таких d', то можно попытаться использовать прямой перебор, чтобы раскрыть шифр. Но все d' различаются множителем, равным НОК(р-1, q-1), и если этот множитель вычислен, то п можно факторизовать. Таким образом, нахождение d' столь же сложно, сколь и факторизация п.

Размещено на Allbest.ru