Поняття про відстань єдиності
Розглянемо декілька інший підхід до поняття стійкості кріптосистеми, яка не залежить від розрахункової потужності опонента, який зв’язан з невизначеністю дешифрування при відомому ключі.
Будемо вважати, що опоненту відома кріптограма Е та опис системи шифрування-дешифрування симетричної кріптосистеми, тобто функції f(M,K) та g(E,K), але невідомий ключ К. Використовуючи до прийнятої кріптограми Е усі можливі ключі К, можна спробувати відновити повідомлення, коли серед численності ключів тільки один є вірним, тоді як інші - помилкові. Відбраковку ключів можна виконувати, використовуючи крітерій, який полягає у отриманні осмисленного текста. Однак може статися, що одній кріптограмі будуть відповідати декілька осмисленних розшифровок. У цьому випадку навіть при необмеженій розрахунковій потужності опонента немає засобу, щоб знайти істиний ключ та відновити дійсно зашифроване повідомлення.
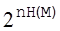 - осмислених "типічних" повідомлень. - осмислених "типічних" повідомлень.
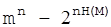 - безглуздих повідомлень. - безглуздих повідомлень.
| 
|
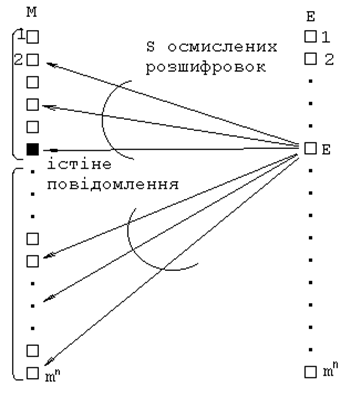
Мал.2.7. Розшифровка кріптограми тотальним перебором ключів.
Нехай одній кріптограмі відповідає S осмислених розшифровок (мал.2.7). З них 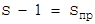 очевидно будуть помилкові, та одна істинна. Передбачемо також, що алфавіти повідомлень та кріптограм, а також довжини послідовностей повідомлень та кріптограм співпадають.
очевидно будуть помилкові, та одна істинна. Передбачемо також, що алфавіти повідомлень та кріптограм, а також довжини послідовностей повідомлень та кріптограм співпадають.
Якщо вдасться побудувати кріптосистему, яка для кожної кріптограми дає дуже велике число помилкових розшифровок, то її можна буде також важати стійкою, оскільки при будь-якій розрахунковій потужності стане неможливим визначити, яка з припущених розшифровок є істинною. Нижня межа для середнього числа помилкових розшифровок 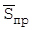 у випадку використання кріптосистеми з ключом довжини N, з об’ємом алфавіта ключових даних L, при шифруванні джерела повідомлення з ентропією Н(М) визначається теоремою Шеннона-Хелмна:
у випадку використання кріптосистеми з ключом довжини N, з об’ємом алфавіта ключових даних L, при шифруванні джерела повідомлення з ентропією Н(М) визначається теоремою Шеннона-Хелмна:
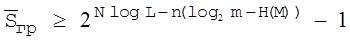 (2.15)
(2.15)
де m - об’єм алфавіта, n - довжина повідомлення (кріптограма). Із даного відношення видно, що якщо показник степені більше нуля та достатньо великий, то середнє число помилкових розшифровок буде дуже великим і систему шифрування можна вважати стійкою.
Але з ростом довжини прийнятої кріптограми та при фіксованому числі ключів, показник степені буде падати і коли він наблизиться до нуля, то можна важати, що помилкових розшифровок не буде, тобто нульове значення показника степені є критичним: при довжині кріптограми 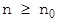 , де
, де 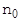 - довжина кріптограми, яка обертає в нуль показник степені, кожна кріптограма може бути розсекречена єдиним чином, а прі
- довжина кріптограми, яка обертає в нуль показник степені, кожна кріптограма може бути розсекречена єдиним чином, а прі 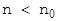 це не так. Величина
це не так. Величина 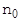 дає ту мінімальну довжину кріптограми, починаючи з якої помилкові розшифровки будуть відсутні, отже, при переборі всіх ключів кожній кріптограмі буде відповідати єдине повідомлення, яке дійсно передавалося. Така довжина кріптограми називається відстанью єдиності
дає ту мінімальну довжину кріптограми, починаючи з якої помилкові розшифровки будуть відсутні, отже, при переборі всіх ключів кожній кріптограмі буде відповідати єдине повідомлення, яке дійсно передавалося. Така довжина кріптограми називається відстанью єдиності 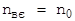 . Знайдемо цю відстань, прирівнюючи до нуля показник степені у (2.15). Розв’язуючи отримане рівняння, знаходимо формулу Шеннона для відстані єдиності.
. Знайдемо цю відстань, прирівнюючи до нуля показник степені у (2.15). Розв’язуючи отримане рівняння, знаходимо формулу Шеннона для відстані єдиності.
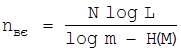 (2.16)
(2.16)
Важливий висновок, вірний для будь-яких кріптосистем, складається у тому, що якщо опонент перехватив кріптограму довжини 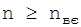 , то він завжди зможе без знання ключа розшифрувати її єдиним правильним чином.
, то він завжди зможе без знання ключа розшифрувати її єдиним правильним чином.
Аналіз формули для відстані єдиності показує, що чим менш надлишковим є джерело, тобто чим більше Н(М) до logm, тим більше відстань єдиності. Використовуючи дану формулу неважко побачити, що для дійсних повідомлень з надлишковістю та при відносно невеликій довжині ключа відстань єдиності є прийнятною для аналізу з боку опонента.
Пример. Пусть алфавит сообщения содержит 32 буквы, а энтропия сообщения H(M) = 1,5 (что примерно соответствует энтропии русского языка). Тогда при двоичном ключе длиною N = 128 символов, расстояние единственности составляет 40 букв.
Зазначимо, що хоча висновок для величини відстані єдиності був приблизним, практичний досвід свідчить, що відстань єдиності має величину того ж порядку, що дає формула Шеннона.
В заключение следует сделать общий вывод о том, что стойкие системы шифрования, криптоанализ которых не зависит от вычислительных или аппаратных возможностей оппонента, к сожалению не реализуемы на коротких ключах (N << n).
Дата добавления: 2016-02-24; просмотров: 767;
