Лекція 7. Частотні критерії стійкості
План лекції:
1. Частотний критерій стійкості Михайлова.
2. Частотний критерій стійкості Найквіста.
Література: [1], [3], [4], [7].
Частотні критерії стійкості належать до графоаналітичних методів. Стійкість системи оцінюється за характером годографа частотної характеристики. Перевагою цього методу є його наочність і можливість експериментального визначення частотних характеристик як для окремих ланок, так і для всієї САК. Це дуже важливо тоді, коли важко скласти диференціальні рівняння для окремих ланок системи.
Частотними критеріями легко можна користуватися для визначення стійкості систем якого завгодно високого порядку. Для дослідження стійкості замкнених САК застосовується критерій Михайлова, а для розімкнених – критерій Найквіста.
1. Частотний критерій стійкості Михайлова. У 1983 році радянський учений А.В.Михайлов запропонував частотний критерій стійкості. Ґрунтується цей метод на взаємозв’язку між характером перехідних процесів, які виникають при порушенні рівноваги системи, й амплітудою та фазою вимушених коливань, що встановлюються в системі під впливом синусоїдної збурюючої дії.
Нехай характеристичне рівняння замкненої системи має вигляд
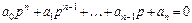 .
.
Якщо замість оператора p підставити 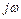 , дістанемо многочлен Михайлова:
, дістанемо многочлен Михайлова:
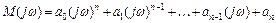 .
.
Очевидно, що многочлен має як дійсну, так і уявну частини:
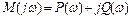 .
.
Якщо задатися різними значеннями 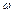 , знайдемо координати кінця вектора Михайлова на комплексній площині. З’єднавши відповідні точки, дістанемо криву, яка називається годографом Михайлова.
, знайдемо координати кінця вектора Михайлова на комплексній площині. З’єднавши відповідні точки, дістанемо криву, яка називається годографом Михайлова.
Як приклад перевіримо, користуючись критерієм Михайлова, стійкість замкненої САК, характеристичне рівняння якої має такий вигляд:
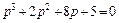 .
.
Многочлен Михайлова для цієї системи:
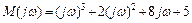 ,
,
або
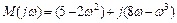 .
.
Надамо 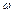 різних значень (від 0 до
різних значень (від 0 до 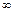 ) і зведемо результати обчислень у таблицю.
) і зведемо результати обчислень у таблицю.
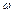
| 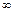
| |||||
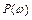
| -3 | -13 | -27 | 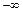
| ||
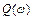
| -3 | -32 | 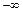
|
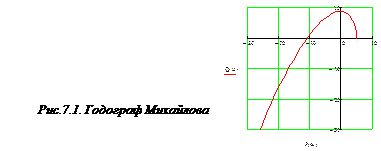 За даними таблиці будуємо годограф Михайлова в комплексній площині, відкладаючи значення
За даними таблиці будуємо годограф Михайлова в комплексній площині, відкладаючи значення 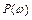 по дійсній осі, а значення
по дійсній осі, а значення 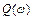 по уявній (рис.7.1).
по уявній (рис.7.1).
Не важко помітити, що годограф Михайлова послідовно проходить через три квадранти проти стрілки годинника і прямує в нескінченність. Отже, розглядувана замкнена САК є стійкою.
Критерій Михайлова формулюється так: САК стійка, якщо годограф Михайлова для неї при зміні частоти від нуля до нескінченності послідовно проходить проти стрілки годинника через n-квадрантів комплексної площини, ніде не перетворюючись у нуль (n – степінь характеристичного рівняння САК).
Дата добавления: 2016-03-27; просмотров: 1010;
