O Закінчити побудову графіків за допомогою кнопки Готово (Finish).
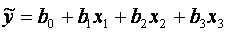 ,
де y – роздрібний товарообіг,
х 1 – кількість підприємств роздрібної торгівлі,
х 2 – всі надані платні послуги,
х 3 – обсяг укладених угод на біржах.
2) Обчислити множинний коефіцієнт детермінації
,
де y – роздрібний товарообіг,
х 1 – кількість підприємств роздрібної торгівлі,
х 2 – всі надані платні послуги,
х 3 – обсяг укладених угод на біржах.
2) Обчислити множинний коефіцієнт детермінації 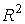 .
3) Обчислити множинний коефіцієнт кореляції
.
3) Обчислити множинний коефіцієнт кореляції 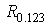 .
4) Перевірити модель на адекватність з ймовірністю р = 0,99.
5) Розрахувати точковий прогноз та з надійністю ?=0,01 побудувати довірчий інтервал для прогнозу (значення прогнозних факторних значень задається студентом).
6) Дати економетричну інтерпретацію одержаних результатів.
Початкові дані:
Див. додаток 2.
Теоретичні відомості
1) ЗНАХОДЖЕННЯ
.
4) Перевірити модель на адекватність з ймовірністю р = 0,99.
5) Розрахувати точковий прогноз та з надійністю ?=0,01 побудувати довірчий інтервал для прогнозу (значення прогнозних факторних значень задається студентом).
6) Дати економетричну інтерпретацію одержаних результатів.
Початкові дані:
Див. додаток 2.
Теоретичні відомості
1) ЗНАХОДЖЕННЯ 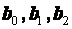 , b 3
За методом найменших квадратів коефіцієнти b 0 , b 1 , b 2, b 3рівняння множинної регресії
, b 3
За методом найменших квадратів коефіцієнти b 0 , b 1 , b 2, b 3рівняння множинної регресії 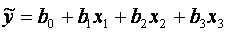 є розв язками системи нормальних рівнянь –системи 4-х лінійних рівнянь з 4 невідомими:
є розв язками системи нормальних рівнянь –системи 4-х лінійних рівнянь з 4 невідомими:
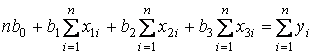
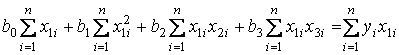 (2.1)
(2.1)
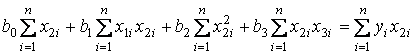
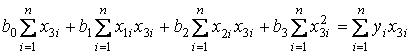 Економічна інтерпретація параметрів рівняння множинної лінійної регресії
Економічна інтерпретація параметрів рівняння множинної лінійної регресії 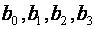 · Значення вільного члена коефіцієнта регресії
· Значення вільного члена коефіцієнта регресії 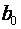 економічного змісту не має.
· Значення коефіцієнта регресії
економічного змісту не має.
· Значення коефіцієнта регресії 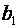 показує, що при збільшенні значення х 1 (кількості підприємств роздрібної торгівлі) на 1 і деякому фіксованому (середньому) значенні
показує, що при збільшенні значення х 1 (кількості підприємств роздрібної торгівлі) на 1 і деякому фіксованому (середньому) значенні 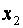 (всіх наданих платних послуг) та
(всіх наданих платних послуг) та 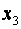 (обсягу укладених угод на біржах) очікується збільшення середнього значення
(обсягу укладених угод на біржах) очікується збільшення середнього значення 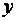 (роздрібного товарообігу) на
(роздрібного товарообігу) на 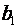 тис.грн.
· Значення коефіцієнта регресії
тис.грн.
· Значення коефіцієнта регресії 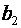 показує, що при збільшенні значення х 2 (всіх наданих платних послуг) на 1 тис.грн. і деякому фіксованому (середньому) значенні
показує, що при збільшенні значення х 2 (всіх наданих платних послуг) на 1 тис.грн. і деякому фіксованому (середньому) значенні 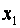 (кількості підприємств роздрібної торгівлі) та
(кількості підприємств роздрібної торгівлі) та 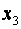 (обсягу укладених угод на біржах) очікується збільшення середнього значення
(обсягу укладених угод на біржах) очікується збільшення середнього значення 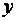 (роздрібного товарообігу) на
(роздрібного товарообігу) на 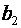 тис. грн.
· Значення коефіцієнта регресії
тис. грн.
· Значення коефіцієнта регресії 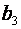 показує, що при збільшенні значення
показує, що при збільшенні значення 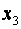 (обсягу укладених угод на біржах) на 1 тис.грн. і деякому фіксованому (середньому) значенні
(обсягу укладених угод на біржах) на 1 тис.грн. і деякому фіксованому (середньому) значенні 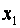 (кількості підприємств роздрібної торгівлі) та х 2 (всіх наданих платних послуг) очікується збільшення середнього значення
(кількості підприємств роздрібної торгівлі) та х 2 (всіх наданих платних послуг) очікується збільшення середнього значення 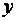 (роздрібного товарообігу) на
(роздрібного товарообігу) на 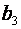 тис. грн.
2) МНОЖИННИЙ КОЕФІЦІЄНТ ДЕТЕРМІНАЦІЇ R 2
тис. грн.
2) МНОЖИННИЙ КОЕФІЦІЄНТ ДЕТЕРМІНАЦІЇ R 2
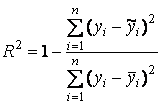 Економічна інтерпретація множинного коефіцієнта детермінації : значення коефіцієнта
Економічна інтерпретація множинного коефіцієнта детермінації : значення коефіцієнта 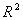 вказує, на скільки % зміна або дисперсія середнього значення обсягу роздрібного товарообігу залежить від зміни або дисперсії значень кількості підприємств роздрібної торгівлі, всіх наданих платних послуг та обсягу укладених угод на біржах в сукупності.
3) МНОЖИННИЙ КОЕФІЦІЄНТ КОРЕЛЯЦІЇ
вказує, на скільки % зміна або дисперсія середнього значення обсягу роздрібного товарообігу залежить від зміни або дисперсії значень кількості підприємств роздрібної торгівлі, всіх наданих платних послуг та обсягу укладених угод на біржах в сукупності.
3) МНОЖИННИЙ КОЕФІЦІЄНТ КОРЕЛЯЦІЇ  –
вказує на щільність або тісноту кореляційного зв язку між роздрібним товарообігом та кількістю підприємств роздрібної торгівлі, всіма наданими платними послугами і обсягом укладених угод на біржах в сукупності.
4) F-КРИТЕРІЙрозраховується для оцінки адекватності моделі, тобто її відповідності емпіричним даним.
–
вказує на щільність або тісноту кореляційного зв язку між роздрібним товарообігом та кількістю підприємств роздрібної торгівлі, всіма наданими платними послугами і обсягом укладених угод на біржах в сукупності.
4) F-КРИТЕРІЙрозраховується для оцінки адекватності моделі, тобто її відповідності емпіричним даним.
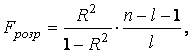
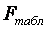 для
для 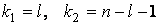 , l – кількість факторів .
Економічна інтерпретація :
Якщо F розр > F табл, то із ймовірністю р можна вважати, що розглянута математична модель адекватна емпіричним даним.
Якщо F розр < F табл, то із ймовірністю р можна вважати, що розглянута математична модель неадекватна емпіричним даним.
5) ДОВІРЧИЙ ІНТЕРВАЛ ДЛЯ ПРОГНОЗУ
, l – кількість факторів .
Економічна інтерпретація :
Якщо F розр > F табл, то із ймовірністю р можна вважати, що розглянута математична модель адекватна емпіричним даним.
Якщо F розр < F табл, то із ймовірністю р можна вважати, що розглянута математична модель неадекватна емпіричним даним.
5) ДОВІРЧИЙ ІНТЕРВАЛ ДЛЯ ПРОГНОЗУ
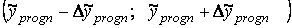
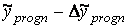 – нижня межа довірчого інтервалу ;
– нижня межа довірчого інтервалу ;
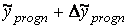 – верхня межа довірчого інтервалу .
– верхня межа довірчого інтервалу .
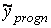 – прогнозне значення показника – ( точковий прогноз )–
– прогнозне значення показника – ( точковий прогноз )– 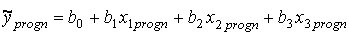 знаходиться безпосереднім обчисленням роздрібного товарообігу за формулою рівняння множинної лінійної регресії при певних значеннях кількості підприємств роздрібної торгівлі, всіх наданих платних послуг та обсягу укладених угод на біржах.
знаходиться безпосереднім обчисленням роздрібного товарообігу за формулою рівняння множинної лінійної регресії при певних значеннях кількості підприємств роздрібної торгівлі, всіх наданих платних послуг та обсягу укладених угод на біржах.
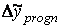 – гранична похибка.
– гранична похибка.
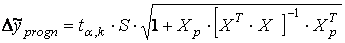 ,
де
,
де 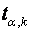 – табличне значення Стьюдента при ?=1 – p та k = n ,
– табличне значення Стьюдента при ?=1 – p та k = n ,
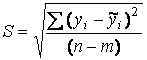 – незміщена оцінка дисперсії залишків
( m – кількість параметрів моделі).
ХІД РОБОТИ в Excel
Крок 1. ЗНАХОДЖЕННЯ КОЕФІЦІЄНТІВ РІВНЯННЯ МНОЖИННОЇ ЛІНІЙНОЇ РЕГРЕСІЇ
– незміщена оцінка дисперсії залишків
( m – кількість параметрів моделі).
ХІД РОБОТИ в Excel
Крок 1. ЗНАХОДЖЕННЯ КОЕФІЦІЄНТІВ РІВНЯННЯ МНОЖИННОЇ ЛІНІЙНОЇ РЕГРЕСІЇ 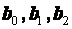 , b 3
Спосіб 1. Розв'язування системи нормальних рівнянь.
У матричній формі розв язки системи нормальних рівнянь (2.1) отримуємо, помноживши обернену матрицю до матриці системи на стовпчик вільних членів.
Х = A -1 ? В,
де А– матриця з коефіцієнтів системи нормальних рівнянь – значень відповідних сум:
A=
, b 3
Спосіб 1. Розв'язування системи нормальних рівнянь.
У матричній формі розв язки системи нормальних рівнянь (2.1) отримуємо, помноживши обернену матрицю до матриці системи на стовпчик вільних членів.
Х = A -1 ? В,
де А– матриця з коефіцієнтів системи нормальних рівнянь – значень відповідних сум:
A= 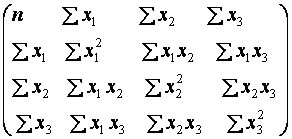 , (2.2)
В –стовпчик з вільних членів системи
В=
, (2.2)
В –стовпчик з вільних членів системи
В= 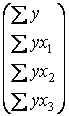 (2.3)
Х– стовпчик шуканих параметрів
Х=
(2.3)
Х– стовпчик шуканих параметрів
Х= 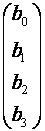 .
Щоб сформувати матрицю Аі стовпчик Вта розв'язати матричним способом систему нормальних рівнянь, потрібно виконати наступні дії:
1)Створити матриц і з вихідних даних :
.
Щоб сформувати матрицю Аі стовпчик Вта розв'язати матричним способом систему нормальних рівнянь, потрібно виконати наступні дії:
1)Створити матриц і з вихідних даних :
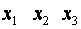 y
Х=
y
Х= 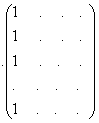 , Y=
, Y= 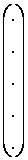 .
Х– матриця розміром n ? 4; 1-й стовпчик складається з 1 (одиниць), 2-й, 3-й і 4-й стовпці – вихідні данідля факторних змінних х 1 , х 2 та х 3;
Y –матриця-стовпчик з емпіричних значень показника у ;
2)виділити порожні комірки розміром 4? n ;
3)транспонувати матрицю Х у ці комірки за допомогою функції
f x ® LookUp & Reference ® Transpose
( або f x ® Ссылки и массивы ® Трансп )
X T =
.
Х– матриця розміром n ? 4; 1-й стовпчик складається з 1 (одиниць), 2-й, 3-й і 4-й стовпці – вихідні данідля факторних змінних х 1 , х 2 та х 3;
Y –матриця-стовпчик з емпіричних значень показника у ;
2)виділити порожні комірки розміром 4? n ;
3)транспонувати матрицю Х у ці комірки за допомогою функції
f x ® LookUp & Reference ® Transpose
( або f x ® Ссылки и массивы ® Трансп )
X T = 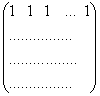 –матриця, транспонована до матриці Х ; розмірність X T – 4? n ;
4)виділити порожні комірки розміром 4 ? 4;
5)виконати множення м атриць X T та Хза допомогою функції
f x ® Math & Trig ® M Mult
(або f x ® Математические ® МУмнож ) ;
!Результат X T ? X– матриця моментіврозміром 4 ? 4 (добуток матриць Х T і Х) – матриця системи нормальних рівнянь, тобто
X T ? X = А;
6)виділити порожні комірки розміром 4 ? 1;
7)виконати множення м атриць X T та Yза допомогою функції M Mult ;
! X T ? Y– матриця розміром 4 ? 1 (добуток матриці Х T і стовпця Y ) – стовпчик вільних членів системи нормальних рівнянь, тобто
X T Y = В ;
8) стовпчик
–матриця, транспонована до матриці Х ; розмірність X T – 4? n ;
4)виділити порожні комірки розміром 4 ? 4;
5)виконати множення м атриць X T та Хза допомогою функції
f x ® Math & Trig ® M Mult
(або f x ® Математические ® МУмнож ) ;
!Результат X T ? X– матриця моментіврозміром 4 ? 4 (добуток матриць Х T і Х) – матриця системи нормальних рівнянь, тобто
X T ? X = А;
6)виділити порожні комірки розміром 4 ? 1;
7)виконати множення м атриць X T та Yза допомогою функції M Mult ;
! X T ? Y– матриця розміром 4 ? 1 (добуток матриці Х T і стовпця Y ) – стовпчик вільних членів системи нормальних рівнянь, тобто
X T Y = В ;
8) стовпчик 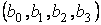 – розв язок с и стеми нормальних рівнянь – може бути знайдений за формулою (у матричному вигляді):
– розв язок с и стеми нормальних рівнянь – може бути знайдений за формулою (у матричному вигляді):
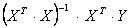 або A -1 ? В
8. 1) знайти обернену матрицю А -1 :
o виділити діапазон порожніх комірок 4 ? 4 – 4 рядки і 4 стовпці;
o вибрати з майстра функцій f x ® Math & Trig ® MInversе
(або f x ® Математические ® МОбр ) ;
o у діалоговому вікні функції MInverse потрібно ввести матрицю Аз коефіцієнтів системи нормальних рівнянь ;
o натиснути клавіші F2, Ctrl+Shift+Enter;
8. 2) помножити матрицю А -1 на стовпчик В:
o виділити діапазон порожніх комірок – стовпець 4 ? 1;
o вибрати з майстра функцій f x ® Math & Trig ® M Mult
(або f x ® Математические ® МУмнож ) ;
o у діалоговому вікні функції MMult потрібно ввести два масиви: обернену матрицю А -1 та стовпчик вільних членів В ;
o натиснути клавіші F2, Ctrl+Shift+Enter.
!Отриманий стовпчик – це стовпчик шуканих параметрів
або A -1 ? В
8. 1) знайти обернену матрицю А -1 :
o виділити діапазон порожніх комірок 4 ? 4 – 4 рядки і 4 стовпці;
o вибрати з майстра функцій f x ® Math & Trig ® MInversе
(або f x ® Математические ® МОбр ) ;
o у діалоговому вікні функції MInverse потрібно ввести матрицю Аз коефіцієнтів системи нормальних рівнянь ;
o натиснути клавіші F2, Ctrl+Shift+Enter;
8. 2) помножити матрицю А -1 на стовпчик В:
o виділити діапазон порожніх комірок – стовпець 4 ? 1;
o вибрати з майстра функцій f x ® Math & Trig ® M Mult
(або f x ® Математические ® МУмнож ) ;
o у діалоговому вікні функції MMult потрібно ввести два масиви: обернену матрицю А -1 та стовпчик вільних членів В ;
o натиснути клавіші F2, Ctrl+Shift+Enter.
!Отриманий стовпчик – це стовпчик шуканих параметрів 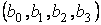 .
Спосіб 2. Застосування функції LINEST.
§ Для отримання результатів потрібно попередньо відмітити 5 рядків і 4 стовпці ( l =4 – кількість параметрів рівняння регресії);
§ У майстрі функцій потрібно вибрати функцію f x ® Statistical ® LINEST ;
§ У діалоговому вікні ввести послідовно:
u відомі_значення_у (виділити вихідні значення показника у)
u відомі_значення_х (виділити вихідні значення факторів х 1 , х 2 , х 3 )
u конст = 1
u статистика = 1 ;
§ Натиснути клавіші: F2, Ctrl+Shift+Enter.
Спосіб 3. Виконання вбудованого модуля регресійного аналізу
TOOLS – DATA ANALYSIS – REGRESSION
(або СЕРВИС – АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ).
u У головному меню потрібно вибрати пункт TOOLS (СЕРВИС), у підменю – пункт DATA ANALYSIS (АНАЛИЗ ДАННЫХ), далі – підпункт REGRESSION (РЕГРЕССИЯ).
u У діалоговому вікні задати залежн у ( y ) та незалежні ( x 1 , x 2 , x 3 ) змінні та рівень надійності ( p = 0,99).
Увага ! Якщо в переліку функцій пункту меню TOOLS (СЕРВИС) немає підпункту DATA ANALYSIS (АНАЛИЗ ДАННЫХ), то його потрібно додати за допомогою ADD / INS (НАДСТРОЙКИ) і вибрати підпункт ANALYSIS TOOLPACK (ПАКЕТ АНАЛИЗА ).
Крок 2. МНОЖИННИЙ КОЕФІЦІЄНТ ДЕТЕРМІНАЦІЇ
.
Спосіб 2. Застосування функції LINEST.
§ Для отримання результатів потрібно попередньо відмітити 5 рядків і 4 стовпці ( l =4 – кількість параметрів рівняння регресії);
§ У майстрі функцій потрібно вибрати функцію f x ® Statistical ® LINEST ;
§ У діалоговому вікні ввести послідовно:
u відомі_значення_у (виділити вихідні значення показника у)
u відомі_значення_х (виділити вихідні значення факторів х 1 , х 2 , х 3 )
u конст = 1
u статистика = 1 ;
§ Натиснути клавіші: F2, Ctrl+Shift+Enter.
Спосіб 3. Виконання вбудованого модуля регресійного аналізу
TOOLS – DATA ANALYSIS – REGRESSION
(або СЕРВИС – АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ).
u У головному меню потрібно вибрати пункт TOOLS (СЕРВИС), у підменю – пункт DATA ANALYSIS (АНАЛИЗ ДАННЫХ), далі – підпункт REGRESSION (РЕГРЕССИЯ).
u У діалоговому вікні задати залежн у ( y ) та незалежні ( x 1 , x 2 , x 3 ) змінні та рівень надійності ( p = 0,99).
Увага ! Якщо в переліку функцій пункту меню TOOLS (СЕРВИС) немає підпункту DATA ANALYSIS (АНАЛИЗ ДАННЫХ), то його потрібно додати за допомогою ADD / INS (НАДСТРОЙКИ) і вибрати підпункт ANALYSIS TOOLPACK (ПАКЕТ АНАЛИЗА ).
Крок 2. МНОЖИННИЙ КОЕФІЦІЄНТ ДЕТЕРМІНАЦІЇ 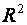 обчислюється за таким алгоритмом:
· обчислити середнє значення
обчислюється за таким алгоритмом:
· обчислити середнє значення 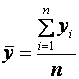 ( f x ® Statistical ® Average) ;
· обчислити в окремому стовпці теоретичні значення показника
( f x ® Statistical ® Average) ;
· обчислити в окремому стовпці теоретичні значення показника 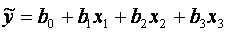 ;
· сформувати стовпці
;
· сформувати стовпці 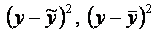 ;
· обчислити суми
;
· обчислити суми 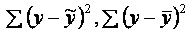 ;
· обчислити коефіцієнт детермінації
;
· обчислити коефіцієнт детермінації 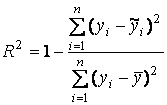 .
Крок 3. МНОЖИННИЙ КОЕФІЦІЄНТ КОРЕЛЯЦІЇ
.
Крок 3. МНОЖИННИЙ КОЕФІЦІЄНТ КОРЕЛЯЦІЇ 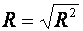 обчислюється для оцінки щільності зв'язку.
Крок 4. ОЦІНКА МОДЕЛІ НА АДЕКВАТНІСТЬ ДО ВИХІДНИХ ДАНИХ
u розрахувати значення
обчислюється для оцінки щільності зв'язку.
Крок 4. ОЦІНКА МОДЕЛІ НА АДЕКВАТНІСТЬ ДО ВИХІДНИХ ДАНИХ
u розрахувати значення 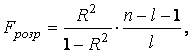 u знайти
u знайти 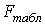 в таблиці критичних точок F -розподілу для ймовірності р =0,99 для
в таблиці критичних точок F -розподілу для ймовірності р =0,99 для 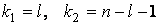 , l – кількість факторів.
Крок 5. ЗНАХОДЖЕННЯ ПРОГНОЗУ
Точковий прогноз
, l – кількість факторів.
Крок 5. ЗНАХОДЖЕННЯ ПРОГНОЗУ
Точковий прогноз 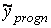 обчислюється за рівнянням регресії
обчислюється за рівнянням регресії
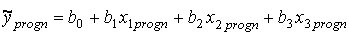 .
Інтервальний прогноз
розраховується за кілька кроків :
1. Знайти з таблиці розподілу Стьюдента
.
Інтервальний прогноз
розраховується за кілька кроків :
1. Знайти з таблиці розподілу Стьюдента 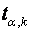 при ?=0,0 1 та k = n ;
2.
при ?=0,0 1 та k = n ;
2. 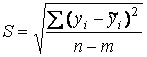 – незміщену оцінку дисперсії залишків ( m – к - сть параметрів );
3. Знайти
– незміщену оцінку дисперсії залишків ( m – к - сть параметрів );
3. Знайти  :
3.1. Сформувати матрицю Х, стовпцями якої є 1 та факторні дані x i .,
3.2. Знайти транспоновану до неї матрицю Х Т за допомогою функції
f x ® LookUp & Reference ® Transpose,
3.3. Обчислити добуток матриць Х Т Х ( f x ® Math & Trig ® Mmult ),
3.4. Знайти обернену матрицю
:
3.1. Сформувати матрицю Х, стовпцями якої є 1 та факторні дані x i .,
3.2. Знайти транспоновану до неї матрицю Х Т за допомогою функції
f x ® LookUp & Reference ® Transpose,
3.3. Обчислити добуток матриць Х Т Х ( f x ® Math & Trig ® Mmult ),
3.4. Знайти обернену матрицю 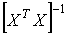 ( f x ® Math & Trig ® MInverse ),
3.5. Сформувати рядок прогнозних факторних значень
Х р = (1 Х 1р rogn Х 2р rogn Х 3 р rogn ),
3.6. Транспонувати цей рядок:
( f x ® Math & Trig ® MInverse ),
3.5. Сформувати рядок прогнозних факторних значень
Х р = (1 Х 1р rogn Х 2р rogn Х 3 р rogn ),
3.6. Транспонувати цей рядок:  3.7. Знайти
3.7. Знайти  – добуток Х р та
– добуток Х р та 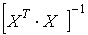 – рядок розміром 1х4 ,
3.8. Обчислити
– рядок розміром 1х4 ,
3.8. Обчислити 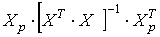 – число , тобто елемент розміром
– число , тобто елемент розміром 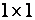 – (добуток рядка
– (добуток рядка 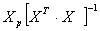 , отриманого в п.3.7 розміром
, отриманого в п.3.7 розміром 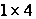 на стовпчик з п.3.6
на стовпчик з п.3.6 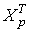 розміром
розміром 
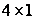 ) ;
4. Обчислити граничну похибку
) ;
4. Обчислити граничну похибку 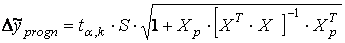 5. Знайти нижню та верхню межі довірчого інтервалу відповідно відніманням та додаванням граничної похибки
5. Знайти нижню та верхню межі довірчого інтервалу відповідно відніманням та додаванням граничної похибки 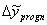 :
:
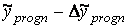 –нижня межа довірчого інтервалу;
–нижня межа довірчого інтервалу;
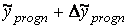 – верхня межа довірчого інтервалу.
– верхня межа довірчого інтервалу.
| Тема 3: МУЛЬТИКОЛІНЕАРНІСТЬ В МНОЖИННІЙ ЛІНІЙНІЙ РЕГРЕСІЇ |
Мета роботи
Після вивчення теми студент повинен знати і виконувати :
1) поняття мультикол інеарності;
2) методи оцінки ступеня мультиколінеарності;
3) вплив мультиколінеарності на характеристики економетричної моделі;
4) методи усунення мудьтиколінеарності;
5) алгоритм Фаррара-Глобера.
Література:
[9, С . 94 -101], [15, С . 31-35, 98-101 ], [16, С . 40-47], [20, С. 138-145],
[25, С . 121-125, 174-188 ].
Завдання
На основі статистичних даних з Додатку 2 необхідно:
- перевірити модель на мультиколінеарність факторних змінних 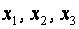 за алгоритмом Фаррара-Глобера.
Початкові дані:
Див. додаток 2.
Теоретичні відомості
МУЛЬТИКОЛІНЕАРНІСТЬ – це існування тісної лінійної залежності або сильної кореляції між двома або більше пояснювальними змінними (факторами) моделі.
Від наявності чи, навпаки, відсутності мультиколінеарності залежить необхідність перетворення чи уточнення переліку пояснювальних змінних.
Ознаки мультиколінеарності:
1. Якщо серед парних коефіцієнтів кореляції пояснюючих змінних є такі, рівень яких наближається до множинного коефіцієнта кореляції або дорівнює йому, це свідчить про можливість існування мультиколінеарності. Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної кореляції, або, як її ще називають, матриця кореляції нульового порядку r. У той же час явище мультиколінеарності в жодному разі не зводиться лише до існування парної кореляції між пояснюючими змінними.
2. Загальніша перевірка передбачає застосування визначника (детермінанта) матриці r , який називається детермінантом кореляції і позначається за алгоритмом Фаррара-Глобера.
Початкові дані:
Див. додаток 2.
Теоретичні відомості
МУЛЬТИКОЛІНЕАРНІСТЬ – це існування тісної лінійної залежності або сильної кореляції між двома або більше пояснювальними змінними (факторами) моделі.
Від наявності чи, навпаки, відсутності мультиколінеарності залежить необхідність перетворення чи уточнення переліку пояснювальних змінних.
Ознаки мультиколінеарності:
1. Якщо серед парних коефіцієнтів кореляції пояснюючих змінних є такі, рівень яких наближається до множинного коефіцієнта кореляції або дорівнює йому, це свідчить про можливість існування мультиколінеарності. Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної кореляції, або, як її ще називають, матриця кореляції нульового порядку r. У той же час явище мультиколінеарності в жодному разі не зводиться лише до існування парної кореляції між пояснюючими змінними.
2. Загальніша перевірка передбачає застосування визначника (детермінанта) матриці r , який називається детермінантом кореляції і позначається 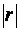 . Числові значення детермінанта кореляції містяться на інтервалі . Числові значення детермінанта кореляції містяться на інтервалі 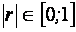 .
Якщо .
Якщо 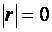 , то існує повна мультиколінеарність.
У разі , то існує повна мультиколінеарність.
У разі 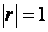 мультиколінеарність відсутня.
Чим ближче мультиколінеарність відсутня.
Чим ближче 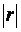 до нуля, тим певніше можна стверджувати, що між пояснюючими змінними існує мультиколінеарність. Незважаючи на те, що числове значення до нуля, тим певніше можна стверджувати, що між пояснюючими змінними існує мультиколінеарність. Незважаючи на те, що числове значення 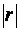 зазнає впливу дисперсії пояснюючих змінних, цей показник можна вважати точковою мірою рівня мультиколінеарності.
3. Коли коефіцієнт детермінації зазнає впливу дисперсії пояснюючих змінних, цей показник можна вважати точковою мірою рівня мультиколінеарності.
3. Коли коефіцієнт детермінації 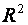 , який обчислено для регресійних залежностей між однією пояснюючою змінною та іншими такими змінними, близький до одиниці, то можна говорити про наявність мультиколінеарності.
4. Якщо , який обчислено для регресійних залежностей між однією пояснюючою змінною та іншими такими змінними, близький до одиниці, то можна говорити про наявність мультиколінеарності.
4. Якщо 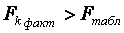 , то , то 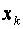 мультиколінеарна з іншими, тобто залежить від інших незалежних змінних і треба вирішити питання про вилучення з переліку змінних однієї з них.
5 . Якщо мультиколінеарна з іншими, тобто залежить від інших незалежних змінних і треба вирішити питання про вилучення з переліку змінних однієї з них.
5 . Якщо 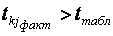 , то , то 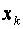 і і 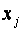 тісно пов язані між собою.
6. Аналізуючи F - і t -критерії, можна зробити висновок, яку із змінних треба вилучити з розгляду в побудованій моделі для усунення мультиколінеарності (треба при цьому виходити і з економіко-логіко-теоретичних міркувань).
ПОКРОКОВИЙ АЛГОРИТМ ФАРРАРА-ГЛОБЕРА
Алгоритм містить три види статистичних критеріїв, на основі яких перевіряється мультиколінеарність:
- усього масиву незалежних змінних ( ? 2 -критерій);
- кожної незалежної змінної з усіма іншими ( F-критерій);
- кожної пари незалежних змінних ( t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають змогу зробити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснюючих змінних.
Крок 1. НОРМАЛІЗАЦІЯ ЗМІННИХ .
Нехай тісно пов язані між собою.
6. Аналізуючи F - і t -критерії, можна зробити висновок, яку із змінних треба вилучити з розгляду в побудованій моделі для усунення мультиколінеарності (треба при цьому виходити і з економіко-логіко-теоретичних міркувань).
ПОКРОКОВИЙ АЛГОРИТМ ФАРРАРА-ГЛОБЕРА
Алгоритм містить три види статистичних критеріїв, на основі яких перевіряється мультиколінеарність:
- усього масиву незалежних змінних ( ? 2 -критерій);
- кожної незалежної змінної з усіма іншими ( F-критерій);
- кожної пари незалежних змінних ( t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають змогу зробити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснюючих змінних.
Крок 1. НОРМАЛІЗАЦІЯ ЗМІННИХ .
Нехай 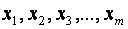 – вектори пояснювальних змінних економетричної моделі. Елементи стандартизованих векторів обчислимо за формулою: – вектори пояснювальних змінних економетричної моделі. Елементи стандартизованих векторів обчислимо за формулою:
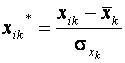 ,
де n – число спостережень ( ,
де n – число спостережень ( 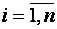 );
m – число пояснювальних (незалежних) змінних ( );
m – число пояснювальних (незалежних) змінних ( 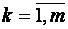 ); );
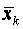 – середня арифметична k -ї пояснювальної змінної; – середня арифметична k -ї пояснювальної змінної;
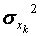 - дисперсія k -ї пояснювальної змінної.
Крок 2 . Знаходження КОРЕЛЯЦІЙНОЇ МАТРИЦІ 1-го порядку - дисперсія k -ї пояснювальної змінної.
Крок 2 . Знаходження КОРЕЛЯЦІЙНОЇ МАТРИЦІ 1-го порядку
 Матриця
Матриця 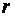 складається з парних коефіцієнтів кореляції, які вказують на щільність кореляційного зв'язку між факторними ознаками.
Знаходиться матриця складається з парних коефіцієнтів кореляції, які вказують на щільність кореляційного зв'язку між факторними ознаками.
Знаходиться матриця 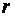 покроково:
– знайти матрицю покроково:
– знайти матрицю 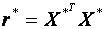 , де , де 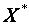 – матриця нормалізованих пояснювальних змінних, а – матриця нормалізованих пояснювальних змінних, а 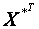 – матриця, транспонована до матриці – матриця, транспонована до матриці 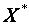 ;
– кореляційна матриця ;
– кореляційна матриця 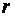 – результат ділення – результат ділення 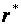 на n .
Крок 3.
1. Визначити на n .
Крок 3.
1. Визначити 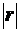 – ВИЗНАЧНИК КОРЕЛЯЦІЙНОЇ МАТРИЦІ r (за допомогою математичної функції MDETERM (МОПРЕД).
2. Обчислити ? 2 -КРИТЕРІЙ ( хі-квадрат ): – ВИЗНАЧНИК КОРЕЛЯЦІЙНОЇ МАТРИЦІ r (за допомогою математичної функції MDETERM (МОПРЕД).
2. Обчислити ? 2 -КРИТЕРІЙ ( хі-квадрат ):
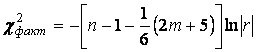 .
3. Значення цього критерію порівнюється з табличним за таких умов: .
3. Значення цього критерію порівнюється з табличним за таких умов: 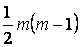 ступенів свободи і рівні значущості ступенів свободи і рівні значущості 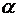 . Якщо . Якщо 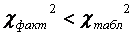 , то в масиві незалежних змінних мультиколінеарність відсутня.
Крок 4. ВИЗНАЧЕННЯ МАТРИЦІ ПОМИЛОК С ( оберненої до r ): , то в масиві незалежних змінних мультиколінеарність відсутня.
Крок 4. ВИЗНАЧЕННЯ МАТРИЦІ ПОМИЛОК С ( оберненої до r ):
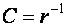 .
Крок 5.
1. РОЗРАХУНОК F-КРИТЕРІЇВ : .
Крок 5.
1. РОЗРАХУНОК F-КРИТЕРІЇВ :
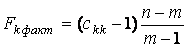 ,
де ,
де 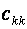 – діагональні елементи матриці С .
2 . Фактичні значення критеріїв – діагональні елементи матриці С .
2 . Фактичні значення критеріїв 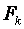 порівнюються з табличними при ( m -1) і ( n-m ) ступенях свободи і рівні значущості порівнюються з табличними при ( m -1) і ( n-m ) ступенях свободи і рівні значущості 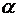 . Якщо . Якщо 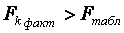 , відповідна k -та пояснююча змінна мультиколінеарна з іншими.
3 . Обчислити коефіцієнти детермінації для кожної змінної: , відповідна k -та пояснююча змінна мультиколінеарна з іншими.
3 . Обчислити коефіцієнти детермінації для кожної змінної:
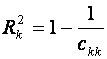 .
Крок 6. Знаходження ЧАСТИННИХ КОЕФІЦІЄНТІВ КОРЕЛЯЦІЇ : .
Крок 6. Знаходження ЧАСТИННИХ КОЕФІЦІЄНТІВ КОРЕЛЯЦІЇ :
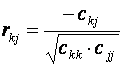 ,
де ,
де 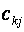 – елементи матриці С, що містяться в k -му рядку і j -му стовпці ( – елементи матриці С, що містяться в k -му рядку і j -му стовпці ( 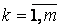 , , 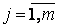 ) , ) , 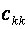 і і 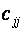 – діагональні елементи матриці С.
Крок 7. РОЗРАХУНОК T-КРИТЕРІЇВ : – діагональні елементи матриці С.
Крок 7. РОЗРАХУНОК T-КРИТЕРІЇВ :
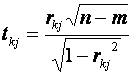 .
Фактичні значення критеріїв .
Фактичні значення критеріїв 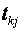 порівнюються з табличними, коли маємо n-m ступенів свободи і рівень значущості порівнюються з табличними, коли маємо n-m ступенів свободи і рівень значущості 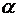 . Якщо . Якщо 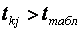 , між змінними , між змінними 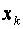 і і 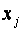 існує мультиколінеарність.
ХІД РОБОТИ в Excel
1. Ввестивихідні статистичні дані(з додатку 2) (роздрібний товарообіг у , кількість підприємств роздрібної торгівлі х 1, всі надані платні послуги х 2та обсяг укладених угод на біржах х 3.
2.Обчислити сумифакторних значень існує мультиколінеарність.
ХІД РОБОТИ в Excel
1. Ввестивихідні статистичні дані(з додатку 2) (роздрібний товарообіг у , кількість підприємств роздрібної торгівлі х 1, всі надані платні послуги х 2та обсяг укладених угод на біржах х 3.
2.Обчислити сумифакторних значень 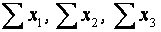 , середні арифметичні значення , середні арифметичні значення 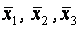 .
3.Сформувати стовпці .
3.Сформувати стовпці 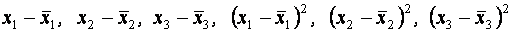 .
4.Обчислити суми .
4.Обчислити суми 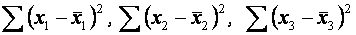 .
5.Знайти середні квадратичні відхиленнядля змінних .
5.Знайти середні квадратичні відхиленнядля змінних 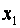 , , 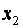 та та 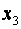 : :
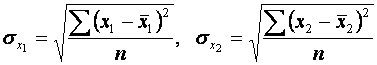 , , 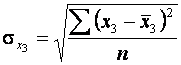 .
6. Нормалізуватизмінні .
6. Нормалізуватизмінні 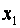 , , 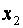 та та 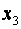 : :
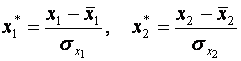 , , 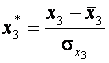 .
Отримані стовпці .
Отримані стовпці 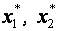 , , 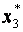 – це матриця – це матриця 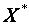 .
7. Транспонуватиматрицю .
7. Транспонуватиматрицю 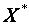 за допомогою вбудованої функції TRANSPOSE( ТРАНСП) із майстра функцій f x ,тип функцій – Look & Referense(Ссылки и массивы) .
Попередньо для отримання транспонованої матриці за допомогою вбудованої функції TRANSPOSE( ТРАНСП) із майстра функцій f x ,тип функцій – Look & Referense(Ссылки и массивы) .
Попередньо для отримання транспонованої матриці 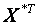 потрібно зарезервувати 3 ? n комірок, тобто 3 рядки і n стовпців.
8. Перемножитиматриці потрібно зарезервувати 3 ? n комірок, тобто 3 рядки і n стовпців.
8. Перемножитиматриці 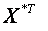 і і 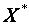 (результат – матриця розміром 3 ? 3).
9.Сформувати кореляційну матрицюr = (результат – матриця розміром 3 ? 3).
9.Сформувати кореляційну матрицюr = 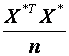 – матрицю парних коефіцієнтів кореляції між факторними змінними. Для цього потрібно кожний елемент матриці – матрицю парних коефіцієнтів кореляції між факторними змінними. Для цього потрібно кожний елемент матриці 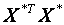 поділити на n = 18.
10.Обчислити визначник кореляційної матриці поділити на n = 18.
10.Обчислити визначник кореляційної матриці 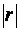 за допомогою функції MDETERM (МОПР)із майстра функцій f x ,тип функцій – Math & Trig(Математические) .
11.Обчислити за допомогою функції MDETERM (МОПР)із майстра функцій f x ,тип функцій – Math & Trig(Математические) .
11.Обчислити 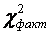
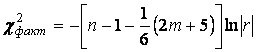 ,
де m – число пояснювальних ( факторних ) змінних.
Значення цього критерію порівнюється з табличним ,
де m – число пояснювальних ( факторних ) змінних.
Значення цього критерію порівнюється з табличним 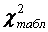 при при 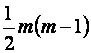 ступенях вільності і рівні значущості ступенях вільності і рівні значущості 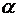 =0,01 (ймовірності р = 0,99). Якщо =0,01 (ймовірності р = 0,99). Якщо 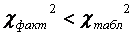 , то в масиві незалежних змінних мультиколінеарність відсутня.
12.Визначити матрицю С , обернену до r (матрицю помилок) : , то в масиві незалежних змінних мультиколінеарність відсутня.
12.Визначити матрицю С , обернену до r (матрицю помилок) :
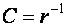 .
13.Розрахувати фактичні значення для критерію Фішера: .
13.Розрахувати фактичні значення для критерію Фішера:
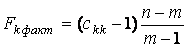 ,
де ,
де 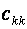 – діагональні елементи матриці С .
Фактичні значення критеріїв – діагональні елементи матриці С .
Фактичні значення критеріїв 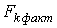 порівняти з табличними при ( m-1) і (n-m) ступенях свободи і рівні значущості порівняти з табличними при ( m-1) і (n-m) ступенях свободи і рівні значущості 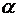 . Якщо . Якщо 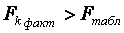 , відповідна k -та пояснююча змінна мультиколінеарна з іншими.
14.Обчислити коефіцієнти детермінаціїдля кожної змінної , відповідна k -та пояснююча змінна мультиколінеарна з іншими.
14.Обчислити коефіцієнти детермінаціїдля кожної змінної
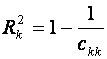 .
15.Знайти частинні коефіцієнтів кореляції: .
15.Знайти частинні коефіцієнтів кореляції:
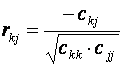 ,
де ,
де 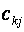 – елементи матриці С, що містяться в k -му рядку і j -му стовпці ( – елементи матриці С, що містяться в k -му рядку і j -му стовпці ( 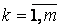 , , 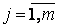 ) , ) , 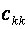 і і 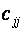 – діагональні елементи матриці С.
16. Розрахунок t-критеріїв: – діагональні елементи матриці С.
16. Розрахунок t-критеріїв:
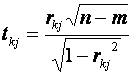 .
Фактичні значення критеріїв .
Фактичні значення критеріїв 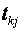 порівнюються з табличними, коли маємо n-m ступенів свободи і рівень значущості порівнюються з табличними, коли маємо n-m ступенів свободи і рівень значущості 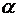 . Якщо . Якщо 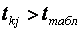 , між змінними , між змінними 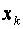 і і 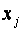 існує мультиколінеарність.
17.Розрахувати парні коефіцієнти кореляції існує мультиколінеарність.
17.Розрахувати парні коефіцієнти кореляції 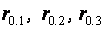 між залежною результуючою змінною y та факторними змінними між залежною результуючою змінною y та факторними змінними 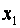 , , 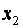 , , 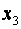 за допомогою функції CORREL(КОРРЕЛ) із майстра функцій f x , тип функцій – Statistical (Статистические) .
18.Зробити висновки щодо існування мультиколінеарностіза трьома видами статистичних критеріїв:
- усього масиву незалежних змінних ( ? 2 -критерій);
- кожної незалежної змінної з усіма іншими ( F-критерій);
- кожної пари незалежних змінних ( t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають змогу зробити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснювальних змінних.
19.У випадку існування мультиколінеарності пояснювальних змінних потрібно одну з них виключати при побудові моделі.
Відкидається з моделі та факторна змінна із підозрілих на мультиколінарність, парний коефіцієнт кореляції якої з результативною ознакою є найменшим. за допомогою функції CORREL(КОРРЕЛ) із майстра функцій f x , тип функцій – Statistical (Статистические) .
18.Зробити висновки щодо існування мультиколінеарностіза трьома видами статистичних критеріїв:
- усього масиву незалежних змінних ( ? 2 -критерій);
- кожної незалежної змінної з усіма іншими ( F-критерій);
- кожної пари незалежних змінних ( t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають змогу зробити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснювальних змінних.
19.У випадку існування мультиколінеарності пояснювальних змінних потрібно одну з них виключати при побудові моделі.
Відкидається з моделі та факторна змінна із підозрілих на мультиколінарність, парний коефіцієнт кореляції якої з результативною ознакою є найменшим.
|
| Тема 4: ПОБУДОВА ЛІНІЙНОЇ ТА ПАРАБОЛІЧНОЇ МОДЕЛЕЙ ТРЕНДУ | ||||||||||||||||||||||||
Мета роботи
Після вивчення теми студент повинен знати і виконувати :
1) загальні типи моделей динаміки;
2) приклади їх застосування в економіці;
3) прогноз на основі моделей часових рядів.
Література:
[11, С . 41 -44, 56-69, 79-82], [13, С . 56 -65], [26, С . 19 -23].
Завдання
На основі даних Додатку 3 необхідно:
1. Побудувати за допомогою методу найменших квадратів лінійну та параболічну моделі трендуекономічного показника у ( за допомогою системи нормальних рівнянь).
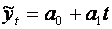
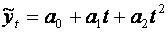 2. Побудувати лінійну та параболічну моделі трендуекономічного показника у за допомогою графіка та контекстного меню Excel .
3. На основі одержаних моделей трендів обчислити прогнозні значення на найближчі два періоди часу.
4. Побудувати графіки емпіричної лінії тренду і теоретичних ліній тренду (лінійної та параболічної).
5. Дати економічну інтерпретацію параметрів трендів і обґрунтувати вибір прогнозних значень досліджуваних економічних показників.
Початкові дані:
Див. додаток 3.
Теоретичні відомості
Прогнозування економічних показників є нагальною потребою в умовах ринкової економіки. У процесі прийняття рішень можливість передбачити майбутню ситуацію є дуже суттєвою для правильного вибору.
Одним з методів прогнозування є знаходження прогнозу на основі моделей тренду за даними часових рядів.
Статистичні прогнози ґрунтуються на гіпотезах про стабільність значень величини, що прогнозується. Основний інструмент прогнозування –екстраполяція . Суть прогнозної екстраполяції полягає в поширенні закономірностей, зв'язків та відношень, виявлених в t -му періоді, за його межі.
1.1. ПОБУДОВА ЛІНІЙНОЇ МОДЕЛІ ТРЕНДУ
2. Побудувати лінійну та параболічну моделі трендуекономічного показника у за допомогою графіка та контекстного меню Excel .
3. На основі одержаних моделей трендів обчислити прогнозні значення на найближчі два періоди часу.
4. Побудувати графіки емпіричної лінії тренду і теоретичних ліній тренду (лінійної та параболічної).
5. Дати економічну інтерпретацію параметрів трендів і обґрунтувати вибір прогнозних значень досліджуваних економічних показників.
Початкові дані:
Див. додаток 3.
Теоретичні відомості
Прогнозування економічних показників є нагальною потребою в умовах ринкової економіки. У процесі прийняття рішень можливість передбачити майбутню ситуацію є дуже суттєвою для правильного вибору.
Одним з методів прогнозування є знаходження прогнозу на основі моделей тренду за даними часових рядів.
Статистичні прогнози ґрунтуються на гіпотезах про стабільність значень величини, що прогнозується. Основний інструмент прогнозування –екстраполяція . Суть прогнозної екстраполяції полягає в поширенні закономірностей, зв'язків та відношень, виявлених в t -му періоді, за його межі.
1.1. ПОБУДОВА ЛІНІЙНОЇ МОДЕЛІ ТРЕНДУ
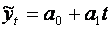 , (*)
де t – час.
Знаходження параметрів , (*)
де t – час.
Знаходження параметрів 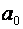 і і 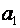 Спосіб 1. Розв'язування системи нормальних рівнянь
Параметри
Спосіб 1. Розв'язування системи нормальних рівнянь
Параметри 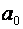 і і 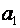 є розв‘язками системи нормальних рівнянь: є розв‘язками системи нормальних рівнянь:
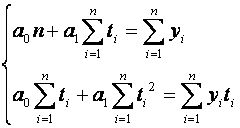 .
У матричній формі система записується наступним чином:
Х ? А=Х 0 ,
де Х – матриця системи, яка складається з коефіцієнтів системи (значень відповідних сум);
Х 0– стовпчик вільних членів;
А – стовпчик шуканих параметрів рівняння тренду .
У матричній формі система записується наступним чином:
Х ? А=Х 0 ,
де Х – матриця системи, яка складається з коефіцієнтів системи (значень відповідних сум);
Х 0– стовпчик вільних членів;
А – стовпчик шуканих параметрів рівняння тренду 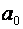 і і 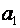 :.
Х = :.
Х = 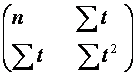 Х 0= Х 0= 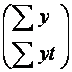 А = А = 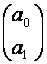 Щоб розв'язати систему нормальних рівнянь в матричній формі, потрібно помножити обернену матрицю X -1 до матриці системи X на стовпчик вільних членів X 0 : А = Х -1 ? X 0 .
Хід роботи
· сформувати таблицю допоміжних значень:
Таблиця 4.1.
Щоб розв'язати систему нормальних рівнянь в матричній формі, потрібно помножити обернену матрицю X -1 до матриці системи X на стовпчик вільних членів X 0 : А = Х -1 ? X 0 .
Хід роботи
· сформувати таблицю допоміжних значень:
Таблиця 4.1.
· сформувати матрицю Х системи нормальних рівнянь Х = · сформувати стовпчик вільних членів системи нормальних рівнянь Х 0= · знайти обернену матрицю Х -1 (за допомогою математичної функції MInverse ( МОбр )); · помножити матрицю Х -1 на стовпчик Х 0 (за допомогою функції M Mult ( МУмнож )). У результаті отримаємо стовпчик розв язків А . Дата добавления: 2016-03-15; просмотров: 1217; |
Генерация страницы за: 0.017 сек.
