Спосіб 1. Розв'язування системи нормальних рівнянь
Аналогічно як при побудові лінійної моделі тренду, параметри параболічної моделі 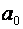 ,
, 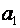 і
і 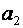 є розв‘язками системи нормальних рівнянь, тільки у даному випадку – системи 3 рівнянь з 3 невідомими:
є розв‘язками системи нормальних рівнянь, тільки у даному випадку – системи 3 рівнянь з 3 невідомими:
.
У матричній формі система записується наступним чином:
Х ? А=Х 0 ,
де Х – матриця системи, яка складається з коефіцієнтів системи (значень відповідних сум);
Х 0– стовпчик вільних членів;
А – стовпчик шуканих параметрів рівняння тренду 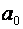 ,
, 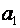 і
і 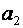 :
:
Х =  , Х 0=
, Х 0=  , А =
, А = 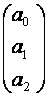 .
.
Шукані параметри рівняння тренду 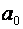 ,
, 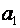 і
і 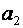 – результат множення оберненої матриці X -1 на стовпчик вільних членів X 0 :
– результат множення оберненої матриці X -1 на стовпчик вільних членів X 0 :
А = Х -1 ? X 0 .
Хід роботи:
!Для формування вихідних матриць Х та Х 0 потрібно взяти значення відповідних сум з допоміжної таблиці розрахунків 4.1.
· сформувати матрицю Х системи нормальних рівнянь
Х =  ;
;
· сформувати стовпчик вільних членів системи нормальних рівнянь
Х 0=  ;
;
· знайти обернену матрицю Х -1 (за допомогою математичної функції MInverse ( МОбр ));
· помножити матрицю Х -1 на стовпчик Х 0 (за допомогою функції M Mult ( МУмнож )). У результаті отримаємо стовпчик розв язків А .
Дата добавления: 2016-03-15; просмотров: 937;
