Спосіб 2. Побудова графіка та застосування контекстного меню 1 страница
Хід роботи:
§ виділити за допомогою миші вихідні дані, тобто стовпчик значень y i ;
§ побудувати графік емпіричної лінії тренду (за допомогою майстра діаграм). Тип графіку – Line (График);
§ стати мишкою на емпіричній лінії тренду і натиснути праву клавішу;
§ у контекстному меню, яке появиться на екрані, вибрати пункт Add TrendLine ( Добавить линию тренда );
§ серед запропонованих ліній тренду вибрати Polinomial (Полиномиальная) і задати степінь = 2 ;
§ у підпункті контекстного меню Option ( Параметры ) виділити такі функції:
o Display equation on chart (Показывать уравнение на диаграмме),
o Display R - square value (Поместить на диаграмму величину достоверности аппроксимации (R 2 ));
§ на екрані появиться графік теоретичної лінії тренду, шукане рівняння тренду та значення коефіцієнту детермінації, яке вказує на довіру до знайденого рівняння тренду.
2.2. Оцінку (прогноз) середнього значення показника у на наступні 2 періоди часу знаходимо:
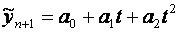 де
де 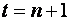 ;
;
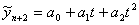 де
де 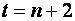 .
.
2.3.Значення параметру 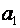 у параболічній моделі тренду (**) показує, що в початковий момент часу (при t =0) очікується збільшення показника у на а 1одиниць за 1 період часу (рік, квартал, чи місяць).
у параболічній моделі тренду (**) показує, що в початковий момент часу (при t =0) очікується збільшення показника у на а 1одиниць за 1 період часу (рік, квартал, чи місяць).
Значення параметра 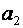 показує, що збільшення економічного показника у в початковий момент часу відбувається з прискоренням, рівним а 2 одиниць .
показує, що збільшення економічного показника у в початковий момент часу відбувається з прискоренням, рівним а 2 одиниць .
Значення 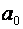 в моделі тренду (**) економічної інтерпретації не має.
в моделі тренду (**) економічної інтерпретації не має.
| ВИКОРИСТАННЯ ВБУДОВАНИХ ФУНКЦІЙ У ВИКОНАННІ ЛАБОРАТОРНИХ РОБІТ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Усі лабораторні завдання курсу „Економетрія розв язуються з використанням персонального комп ютера (ПК). Однією з найбільш орієнтованих під економічні розрахунки є програма EXCEL , яку взято за базову для проведення лабораторних занять.
ФУНКЦІЇ ДЛЯ РОБОТИ З МАТРИЦЯМИ
EXCEL надає кілька функцій для роботи з матрицями, які належать до категорії " Math&Trig" ("Математические").
Перед виконанням функцій над матрицями завжди потрібно резервувати (виділяти) певну кількість комірок для виведення результату.
MINVERSE( Array ) або МОБР( масив ) – функція знаходження оберненої матриці :
· перед використанням функції Minverse знаходження оберненої матриці розмірністю n ? n потрібно зарезервувати (виділити) діапазон комірок ( n рядків і n стовпців), тобто резервується така кількість комірок, яка співпадає із розміром вихідної матриці;
· на панелі інструментів активізувати піктограму майстра фу нкцій f x ;
· серед запропонаваних типів функцій вибрати тип " Math&T rig " ;
· у запропонованому переліку вибрати функцію " Minverse ";
· з'явиться діалогове вікно вводу масиву;
· виділити вихідну матрицю і натиснути ОК;
· у резервованих комірках в лівому верхньому куті з'являється число;
· щоб показати всі числа матриці, потрібно натиснути таку послідовність клавіш: F2, Ctrl+Shift+Enter.
MMULT( Array 1; Array 2 ) або МУМНОЖ( масив 1; масив 2 ) – функція множення матриць , які містяться в масивах. Результат – це масив з таким самим числом рядків, як і масив 1 і таким самим числом стовпців, як і масив 2. Тобто при множенні матриць розміром n ? m i m ? k потрібно виділити n? k комірок. Далі виконати таку послідовність дій:
· f x ® Math & Trig ® MMult ;
· у діалоговому вікні ввести масиви матриць;
· для виведення всього результату на екран натиснути:
F2, Ctrl+Shift+Enter.
MDETERM (Array )або МОПРЕД( масив ) обчислює визначник матриці. Матриця записується у масиві.
TRANSPOSE ( array )або ТРАНСП(масив) – функція знаходження транспонованої матриці . Транспонування полягає в тому, що перший рядок вихідного масиву стає першим стовпцем нового масиву, а другий рядок – другим його стовпцем і т.д.
Перед транспонуванням масиву n ? m потрібно зарезервувати m ? n комірок. Далі:
· f x ® Look & Reference (Ссылки и массивы) ® Transpose (Трансп) ;
· у діалоговому вікні ввести масив вихідної матриці і ОК;
· для виведення всього результату на екран натиснути:
F2, Ctrl+Shift+Enter.
Приклад :
Як приклад роботи з матрицями розглянемо операцію множення матриці (А1:С4) з матрицею (Е1:Е3) розміром 4 ? 3 і 3 ? 1.
Перш ніж звернутися до майстра функцій, потрібно виокремити область, де міситиметься результат множення (G1:G4). Ця область матиме стільки ж рядків, скільки й перша вхідна (у даному прикладі – 4), і стільки ж стовпців, скільки друга (у прикладі – 1). Далі в розділі Майстер функцій вибираємо функцію М Mult із категорії Math & Trig і вводимо вихідні матриці. Після виконання з явиться перший елемент матриці-результату. Для появи інших натиснемо спочатку F2, а потім одночасно Ctrl+Shift+Enter. СТАТИСТИЧНІ ФУНКЦІЇEXCEL . AVERAGE( number 1; number 2; … ) або СРЗНАЧ( число 1; число 2;.. .). Це функція обчислення середнього арифметичного. f x ® Statistical ® Average . VAR( number 1; number 2; … ) або ДИСП( число 1; число 2; ...) (. Ця функція обчислює дисперсію випадково взятих п чисел, причому їх кількість не може перевищувати 30. Функція ДИСП передбачає, що елементи є вибіркою з генеральної сукупності. Якщо дані являють собою більшу сукупність, потрібно використовувати функцію ДИСПР. f x ® Statistical ® Var . STDEV( number 1; number 2; … ) або КВАДРОТКЛ( число 1; число 2;. ..) – сума квадратів відхилень точок даних від їх середнього. Кількість аргументів має не перевищувати 30. Можна використовувати масив чи посилання на масив замість аргументів, що відокремлені крапкою чи комою. f x ® Statistical ® Stdev . CORREL( array 1; array 2; … ) або КОРРЕЛ( масив 1; масив 2 ). Коефіцієнт кореляції між інтервалами клітинок „масив 1 та „масив 2 . Застосовується для визначення щільності лінійного зв язку між двома показниками. f x ® Statistical ® Correl . LINEST( known_y; known _ x ; const ; statistica ) або ЛИНЕЙН( відомі_значення_у; відомі_значення_х; конст; статистика ). Ця функція застосовує метод найменших квадратів, щоб визначити оцінки параметрів b лінійної регресії: Функція може додатково обчислювати регресійну статистику. „ Відомі_значення_у – множина значень у . Якщо масив у має один стовпець, то кожний стовпець масиву „відомі_значення_х інтерпретується як окрема змін н а. Якщо масив „відомі_значення_у має один рядок, то кожний рядок „відомих_значень_х" інтерпретується як окрема змінна. „ Відомі_значення_х – множина значень х, що враховує або одну (парна регресія), або кілька змінних (множинна регресія). Якщо „відомі_значення_хпропустити, то вважається, що це масив {1;2;3;...} такого самого розміру, як п „відомих_значень_у . „ Конст – логічне значення. Якщо „конст" має значення „ ложь або" false ", то b 0 беруть таким, що дорівнює нулю; значення b 0 добирають так, щоб виконувалась рівність Y=X B (модель без вільного члена). Якщо „конст має значення „истина , то b 0 обчислюється традиційно (модель з вільним членом). „ Статистика – логічне значення, яке вказує, чи потрібно обчислювати додаткову статистику за регресію. Якщо „статистика має значення „ истина або " true " , то функція ЛИНЕЙН обчислює додаткову регресійну статистику у вигляді масиву:
де Ступінь свободи дорівнює ( п-т) , де п – кількість спостережень, т – кількість параметрів моделі; це значення необхідне для визначення табличного значення F-критерію; Якщо статистика має значення „ ложь чи її пропустити, то функція ЛИНЕЙН обчислює лише коефіцієнти Результат з явиться на екрані після послідовного натискання таких клавіш: F2, Ctrl+Shift+Enter. |
| ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Економетрія – це наука ...
2. Лінійна парна регресія – це скільки факторна модель?
3. Множинна лінійна регресія – це ...
4. Парна лінійна регресія описується ...
5. Якщо R=0,95 для регресії 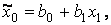 то ...
6. Множинний коефіцієнт детермінації показує, що ...
7. Парний коефіцієнт кореляції вказує на ...
8. Парний коефіцієнт детермінації = ...
9. Економічний зміст коефіцієнту а в регресії то ...
6. Множинний коефіцієнт детермінації показує, що ...
7. Парний коефіцієнт кореляції вказує на ...
8. Парний коефіцієнт детермінації = ...
9. Економічний зміст коефіцієнту а в регресії 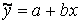 .
10. Коефіцієнт b в регресії .
10. Коефіцієнт b в регресії 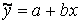 має таке економічне значення:
11. Якщо R =0, то ...
12. Адекватність моделі – це ...
13. Щоб знайти точковий прогноз, потрібно ...
14. Точковий прогноз є точнішим (або менш точним), ніж інтервальний, тому що ...
15. F-критерій обчислюється для того, щоб …
16. Суть методу найменших квадратів.
17. Розв язками системи нормальних рівнянь є ...
18. Коефіцієнт еластичності К для регресії має таке економічне значення:
11. Якщо R =0, то ...
12. Адекватність моделі – це ...
13. Щоб знайти точковий прогноз, потрібно ...
14. Точковий прогноз є точнішим (або менш точним), ніж інтервальний, тому що ...
15. F-критерій обчислюється для того, щоб …
16. Суть методу найменших квадратів.
17. Розв язками системи нормальних рівнянь є ...
18. Коефіцієнт еластичності К для регресії 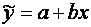 показує, що ...
19. Кореляційним називається зв язок ....
20. У чому полягає відмінність парної і множинної лінійної регресії?
21. Функціональним називається зв язок ....
22. Вкажіть етапи побудови кореляційно-регресійної моделі.
23. Яка економічна інтерпретація параметрів рівняння регресії?
24. Якими показниками вимірюється щільність зв язку?
25. Що виражає коефіцієнт детермінації?
26. Як проводиться статистична оцінка істотності коефіцієнтів регресії та кореляції?
27. Дайте інтерпретацію інтервалу довір я.
28. Тренд – це ...
29. Мультиколінеарність – це ...
30. Основні ознаки мультиколінеарності. показує, що ...
19. Кореляційним називається зв язок ....
20. У чому полягає відмінність парної і множинної лінійної регресії?
21. Функціональним називається зв язок ....
22. Вкажіть етапи побудови кореляційно-регресійної моделі.
23. Яка економічна інтерпретація параметрів рівняння регресії?
24. Якими показниками вимірюється щільність зв язку?
25. Що виражає коефіцієнт детермінації?
26. Як проводиться статистична оцінка істотності коефіцієнтів регресії та кореляції?
27. Дайте інтерпретацію інтервалу довір я.
28. Тренд – це ...
29. Мультиколінеарність – це ...
30. Основні ознаки мультиколінеарності.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ДОДАТКИ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Додаток 1
Дані для виконання лабораторної роботи № 1
" Парна лінійна регресія ":
Y – прибуток фірми, X – інвестиції (в тис. у.о.).
Дані згідно варіанту вибираються студентом відповідно до номера у списку групи.
Дата добавления: 2016-03-15; просмотров: 731; |
Генерация страницы за: 0.019 сек.


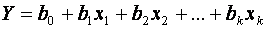 .
.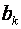
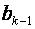
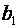
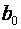
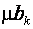
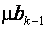
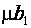
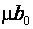
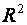
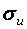
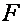
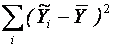
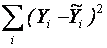
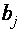 - оцінка параметрів рівняння регресії, j=
- оцінка параметрів рівняння регресії, j= 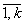 ;
;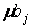 - стандартна похибка оцінки параметра;
- стандартна похибка оцінки параметра;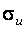 - стандартна похибка залишків;
- стандартна похибка залишків;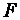 -
- 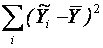 - сума квадратів відхилень, що пояснюється регресією;
- сума квадратів відхилень, що пояснюється регресією;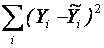 - сума квадратів відхилень, що пояснюється похибкою и .
- сума квадратів відхилень, що пояснюється похибкою и .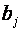 та константу
та константу