Спосіб 2. Побудова графіка та застосування контекстного меню 7 страница
| Регрессионная статистика | Дисперсионный анализ | ||||||||||||
| Множественный R | 0,783 | df | SS | MS | F | Значимость F | |||||||
| R-квадрат | 0,613 | Регрессия | 10355,922 | 3451,97 | 7,406 | 0,0033 | |||||||
| Нормированный R-квадрат | 0,531 | Остаток | 6525,210 | 466,09 | |||||||||
| Стандартная ошибка | 21,589 | Итого | 16881,132 | ||||||||||
| Наблюдения | |||||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 99,0% | Верхние 99,0% | |
| Y-пересечение | -72,581 | 46,936 | -1,546 | 0,144 | -173,249 | 28,087 | -212,302 | 67,140 |
| Переменная X1 | 1,703 | 1,833 | 0,929 | 0,369 | -2,228 | 5,633 | -3,753 | 7,158 |
| Переменная X2 | 9,140 | 2,308 | 3,961 | 0,001 | 4,191 | 14,089 | 2,271 | 16,009 |
| Переменная X3 | 1,641 | 1,974 | 0,832 | 0,420 | -2,592 | 5,875 | -4,235 | 7,517 |
ЗНАХОДЖЕННЯ ПРОГНОЗУ
| Точковий прогноз | Інтервальний прогноз | t pn (p=0,99; n=18) = 2,88 | |||||||||||
| х1 прогн | Х прогн | Х Т прогн | S = | 21,589 | |||||||||
| х2 прогн | Х прогн (X T X) -1 | 0,70 2 | -0,0169 | -0,0385 | 0,0091 | dy = | 68,217 | ||||||
| х3 прогн | Х прогн (X T X) -1 Х Т прогн | 0,20 4 | y прогн - dy = | 3,151 | |||||||||
| у прогн | 71,368 | y прогн + dy = | 139,584 |
ВИСНОВКИ
1. Рівняння множинної лінійної регресії: 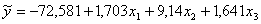
2. Значення вільного члена коефіцієнта регресії b 0 =-42,581 економічного змісту не має.
3. Значення коефіцієнта регресії b 1 =1,703 показує, що при збільшенні кількості підприємств роздрібної торгівлі на 1 і деякому фіксованому (середньому) значенні всіх наданих платних послуг та обсягу укладених угод на біржах очікується збільшення середнього значення роздрібного товарообігу на 1,703 тис. грн.
4. Значення коефіцієнта регресії b 2 =9,14 показує, що при збільшенні значення всіх наданих платних послуг на 1 тис. грн. і деякому фіксованому (середньому) значенні кількості підприємств роздрібної торгівлі та обсягу укладених угод на біржах очікується збільшення середнього значення роздрібного товарообігу на 9,14 тис. грн.
5. Значення коефіцієнта регресії b 3 =1,641 показує, що при збільшенні значення обсягу укладених угод на біржах на 1 тис. грн. і деякому фіксованому значенні кількості підприємств роздрібної торгівлі та всіх наданих платних послуг очікується збільшення середнього значення роздрібного товарообігу на 1,641 тис. грн.
6. R 2 =0,613 вказує, на 61,3% зміна або дисперсія середнього значення обсягу роздрібного товарообігу залежить від зміни кількості підприємств роздрібної торгівлі, всіх наданих платних послуг та обсягу укладених угод на біржах в сукупності і на 38,7% від інших факторів, не врахованих у цій моделі.
7. R =0,783 вказує на тісний кореляційний зв язок між роздрібним товарообігом та кількістю підприємств роздрібної торгівлі, всіма наданими платними послугами і обсягом укладених угод на біржах в сукупності.
8. Оскільки F розр > F табл , то із ймовірністю р=0,99 можна вважати, що розглянута математична модель адекватна емпіричним даним.
Додаток 9
Опис результатів вбудованого модуля REGRESSION
| SUMMARY OUTPUT (Вивід висновків) | ||||||||||||||||||||||||||||
| Regression Statistics | ||||||||||||||||||||||||||||
| Multiple R | 0,762 | – множинний коефіцієнт кореляції | ||||||||||||||||||||||||||
| R Square | 0,581 | – множинний коефіцієнт детермінації | ||||||||||||||||||||||||||
| Adjusted R Square | 0,492 | – нормований множинний коефіцієнт детермінації | ||||||||||||||||||||||||||
| Standard Error | 24,235 | – стандартна похибка рівняння регресії | ||||||||||||||||||||||||||
| Observations | – кількість спостережень | |||||||||||||||||||||||||||
| ANOVA | (ANALYSIS OF VARIANCE) | ДИСПЕРСІЙНИЙ АНАЛІЗ | ||||||||||||||||||||||||||
| df | SS | MS | F | Significance F | ||||||||||||||||||||||||
| Regression | 11416,012 | 3805,337 | 6,479 | 0,006 | ||||||||||||||||||||||||
| Residual | 8222,932 | 587,352 | ||||||||||||||||||||||||||
| Total | 19638,944 | |||||||||||||||||||||||||||
| Кількість ступенів вільності k 1 = m, k2 = n-m-1 (m – кількість параметрів) |
| Середні суми квадратів відхилень (дисперсії) | Розрахункове значення F-критерію | Рівень значущості адекватності моделі | ||||||||||||||||||||||||
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 99,0% | Upper 99,0% | |||||||||||||||||||||
| Intercept | -67,851 | 43,221 | -1,570 | 0,139 | -160,552 | 24,849 | -196,515 | 60,812 | ||||||||||||||||||||
| X Variable 1 | 9,668 | 4,984 | 1,940 | 0,073 | -1,022 | 20,357 | -5,169 | 24,504 | ||||||||||||||||||||
| X Variable 2 | 6,003 | 2,842 | 2,113 | 0,053 | -0,092 | 12,097 | -2,456 | 14,462 | ||||||||||||||||||||
| X Variable 3 | -2,603 | 3,340 | -0,779 | 0,449 | -9,765 | 4,560 | -12,544 | 7,339 | ||||||||||||||||||||
| Коефіцієнти рівняння регресії b0 , b 1 , b 2 , b 3 | Похибки коефіцієнтів регресії | t-статистика (t-критерій Стьюдента) | Перевірка коефіцієнтів на статистичну вірогідність з рівнем значущості P-value або ймовірністю 1-Р | Нижня межа довірчого інтервалу для коефіцієнтів регресії b 0, b 1 , b 2 , b 3 з ймовірністю Р = 0,95 | Верхня межа довірчого інтервалу для коефіцієнта регресії b 0 , b 1 , b 2 , b 3 з ймовірністю Р = 0,95 | Нижня межа довірчого інтервалу коефіцієнта регресії b 0, b 1 , b 2 , b 3 з ймовірністю Р = 0,99 | Верхня межа довірчого інтервалу коефіцієнта регресії b 0, b 1 , b 2 , b 3 з ймовірністю Р = 0,99 | |||||||||||||||||||||
Додаток 10
Зразок Звіт з лабораторної роботи № 3 на тему " Мультиколінеарність в множинній лінійній регресії "
| № | Y | X 1 | Х 2 | Х 3 | X 1 -X 1 сер | X 2 -X 2 сер | X 3 -X 3 сер | (X 1 -X 1 сер ) 2 | (X 2 -X 2 сер ) 2 | (X 3 -X 3 сер ) 2 | X 1 * | X 2 * | X 3 * | ||
| 75,59 | 20,36 | 13,77 | 13,5 | 6,779 | -0,448 | -0,750 | 45,953 | 0,201 | 0,563 | 2,371 | -0,183 | -0,265 | |||
| 60,31 | 12,07 | 11,05 | 13,8 | -1,511 | -3,168 | -0,450 | 2,283 | 10,035 | 0,202 | -0,528 | -1,291 | -0,159 | |||
| 65,61 | 10,98 | 11,9 | 12,6 | -2,601 | -2,318 | -1,650 | 6,766 | 5,372 | 2,723 | -0,910 | -0,945 | -0,584 | |||
| 81,02 | 17,04 | 12,8 | 13,9 | 3,459 | -1,418 | -0,350 | 11,964 | 2,010 | 0,123 | 1,210 | -0,578 | -0,124 | |||
| 70,61 | 12,42 | 12,4 | 12,1 | -1,161 | -1,818 | -2,150 | 1,348 | 3,304 | 4,623 | -0,406 | -0,741 | -0,761 | |||
| 75,69 | 11,98 | 12,7 | 18,2 | -1,601 | -1,518 | 3,950 | 2,564 | 2,304 | 15,603 | -0,560 | -0,619 | 1,397 | |||
| 82,62 | 12,15 | 14,4 | 14,7 | -1,431 | 0,182 | 0,450 | 2,048 | 0,033 | 0,202 | -0,500 | 0,074 | 0,159 | |||
| 103,66 | 15,75 | 13,9 | 14,2 | 2,169 | -0,318 | -0,050 | 4,704 | 0,101 | 0,003 | X* | 0,758 | -0,130 | -0,018 | ||
| 96,68 | 12,3 | 14,5 | 13,9 | -1,281 | 0,282 | -0,350 | 1,641 | 0,080 | 0,123 | -0,448 | 0,115 | -0,124 | |||
| 102,68 | 10,5 | 14,7 | 12,6 | -3,081 | 0,482 | -1,650 | 9,493 | 0,233 | 2,723 | -1,077 | 0,197 | -0,584 | |||
| 110,36 | 10,51 | 14,8 | 11,9 | -3,071 | 0,582 | -2,350 | 9,432 | 0,339 | 5,523 | -1,074 | 0,237 | -0,831 | |||
| 99,34 | 18,42 | 7,9 | 10,6 | 4,839 | -6,318 | -3,650 | 23,415 | 39,914 | 13,323 | 1,692 | -2,575 | -1,291 | |||
| 116,38 | 10,54 | 15,9 | 13,3 | -3,041 | 1,682 | -0,950 | 9,248 | 2,830 | 0,902 | -1,063 | 0,686 | -0,336 | |||
| 130,42 | 16,37 | 16,2 | 14,4 | 2,789 | 1,982 | 0,150 | 7,778 | 3,929 | 0,023 | 0,975 | 0,808 | 0,053 | |||
| 145,59 | 12,97 | 16,8 | 12,7 | -0,611 | 2,582 | -1,550 | 0,373 | 6,668 | 2,403 | -0,214 | 1,052 | -0,548 | |||
| 135,55 | 12,78 | 17,5 | 14,8 | -0,801 | 3,282 | 0,550 | 0,642 | 10,773 | 0,303 | -0,280 | 1,338 | 0,195 | |||
| 152,71 | 15,6 | 17,9 | 15,4 | 2,019 | 3,682 | 1,150 | 4,076 | 13,559 | 1,323 | 0,706 | 1,501 | 0,407 | |||
| 165,02 | 11,72 | 16,8 | 23,9 | -1,861 | 2,582 | 9,650 | 3,464 | 6,668 | 93,123 | -0,651 | 1,052 | 3,414 | |||
| Середнє | 13,581 | 14,218 | 14,250 | 147,193 | 108,352 | 143,805 | |||||||||
| Квадратичні відхилення | 2,860 | 2,453 | 2,827 | ||||||||||||
| 2,371 | -0,528 | -0,910 | 1,210 | -0,406 | -0,560 | -0,500 | 0,758 | -0,448 | -1,077 | -1,074 | 1,692 | -1,063 | 0,975 | -0,214 | -0,280 | 0,706 | -0,651 | ||
| Х* Т | -0,183 | -1,291 | -0,945 | -0,578 | -0,741 | -0,619 | 0,074 | -0,130 | 0,115 | 0,197 | 0,237 | -2,575 | 0,686 | 0,808 | 1,052 | 1,338 | 1,501 | 1,052 | |
| -0,265 | -0,159 | -0,584 | -0,124 | -0,761 | 1,397 | 0,159 | -0,018 | -0,124 | -0,584 | -0,831 | -1,291 | -0,336 | 0,053 | -0,548 | 0,195 | 0,407 | 3,414 |
| Кореляційна матриця | Детермінант кореляційної матриці | Матриця помилок С | |||||||||||||||
| -4,1200596 | -2,80 | -0,229 | -0,156 | determ r | 0,788 | 1,061 | 0,210 | 0,080 | |||||||||
| Х* Т Х* | -4,120 | 7,29 | r | -0,229 | 0,405 | 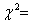
| 3,846 | 0,210 | 1,238 | -0,468 | |||||||
| -2,80 | 7,29 | -0,156 | 0,405 | 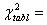
| 11,3 | 0,080 | -0,468 | 1,202 |
| Критерій Фішера | Коефіцієнти детермінації | Частинні коефіцієнти кореляції | t-критерій Стьюдента | Парні коефіцієнти кореляції | |||||||||||
| F 1 | 0,454 | R 1 2 | 0,057 | r 12 | -0,184 | t 12 | -0,724 | r 01 | -0,032 | ||||||
| F 2 | 1,784 | R 2 2 | 0,192 | r 13 | -0,071 | t 13 | -0,275 | r 0 2 | 0,757 | ||||||
| F 3 | 1,516 | R 3 2 | 0,168 | r 23 | 0,384 | t 23 | 1,611 | r 0 3 | 0,423 | ||||||
| F ta bl (?=0,001, k 1 =2, k 2 =15) = 6,36 |
Висновки
1. Детермінант кореляції є ближчим до 1, тому можна стверджувати, що між пояснюючими змінними немає мультиколінеарності.
2.  , що вказує на відсутність мультиколінеарності між факторними ознаками.
, що вказує на відсутність мультиколінеарності між факторними ознаками.
3. Оскільки 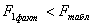 , то
, то 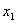 не є мультиколінеарна з іншими.
не є мультиколінеарна з іншими. 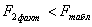 і
і 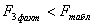 – отже,
– отже, 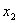 та
та 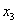 не є мультиколінеарні з іншими.
не є мультиколінеарні з іншими.
4. Значення коефіцієнтів детермінації є близькі до 0,тому можна говорити про відсутність мультиколінеарності.
5. 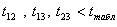 , тому пояснювальні змінні не є пов язані між собою.
, тому пояснювальні змінні не є пов язані між собою.
6. Оскільки між пояснювальними змінними мультиколінеарності немає, то не потрібно вилучати котрусь з факторних ознак з моделі.
Додаток 11
Зразок
Звіт з лабораторної роботи № 4 на тему " Побудова лінійної та параболічної моделі тренду "
| Рік | y | t | t 2 | t 3 | t 4 | yt | yt 2 | |||||||||||
| Сума | ||||||||||||||||||
| ПОБУДОВА ЛІНІЙНОЇ МОДЕЛІ ТРЕНДУ | ||||||||||||||||||
| Спосіб 1 | Розв'язування системи нормальних рівнянь | |||||||||||||||||
| Х | Х 0 | Х -1 | 0,379 | -0,045 | а 0 | -128,575 | ||||||||||||
| -0,045 | 0,007 | а 1 | 77,332 | |||||||||||||||
Дата добавления: 2016-03-15; просмотров: 743;

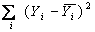
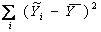
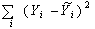 Суми квадратів відхилень
Суми квадратів відхилень