Установившееся движение жидкости и газа в пористой среде.
При установившемся движении каждая точка пространства характеризуется определённой, не изменяющейся во времени скоростью; частицы жидкости и газа придя в любую точку пространства в различные моменты времени, будут иметь в этой точке одну и ту же скорость (постоянную по величине и направлению).
При установившемся движении
V = f (x, y, z, t)
При установившемся движении траектории частиц, проходящие через одну и ту же точку пространства, характеризуются следующим:
эти траектории совпадают друг с другом (сливаются в одну линию);
они являются неизменными во времени.
При установившемся движении жидкости и газа в пористой среде целесообразно рассмотреть три типа фильтрационных потоков.
| |
Законы движения вдоль всех траекторий такого фильтрационного потока совершенно одинаковы, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за декартову ось координат, на пример за ось Х.
В этом случае положение частицы жидкости, движущейся вдоль оси, вполне определяется одной координатой. Кроме того, если рассматривается поток установившийся, то в любой его точке скорость фильтрации и напор будут функциями только одной координаты Х. Поток, обладающий перечисленными свойствами, называется одномерным.
С одномерным фильтрационным потоком приходится сталкиваться на практике в следующих, например, случаях:
в лабораторных условиях при движении жидкости или газа через цилиндрический керн параллельно его оси;
на отдельных участках подземного артезианского потока, когда поперечное сечение потока мало изменяется.
Второй тип Исследование особенностей этого потока имеет весьма большое значение для понимания законов притока нефти, воды и газа к скважинам. Предположим, что при движении жидкости или газа в пористой среде все его частицы движутся параллельно одной и той же плоскости. Такое плоскопараллельное движение частиц жидкости или газа можно назвать двухмерным, ибо для полной характеристики потока достаточно изучить движение хотя бы в одно плоскости, параллельной основной; положение же частиц в определённой плоскости вполне определяется двумя координатами. Если в каждой из упомянутых плоскостей движения траектории оказываются прямыми линиями, радиально сходящимися в одной точке (или расходящимися из одной точки), то такое движение называется двухмерным радиальнымили плоскорадиальным движением.
Как и случае одномерного потока, частицы жидкости или газа здесь движутся по прямолинейным траекториям, но в основной плоскости движения траектории, а следовательно, и скорости фильтрации друг другу непараллельны.
В произвольном установившемся плоско-параллельном (двухмерном) потоке скорость фильтрации и напор должны быть, вообще говоря, функциями двух координат, определяющих положение точки в плоскости потока.
Однако в частном случае плоско-радиального потока картина упрощается: благодаря осевой симметрии величина скорости фильтрации и напор в какой угодно точке потока зависит только от её расстояния до точки пересечения всех траекторий, лежащих в одной плоскости с этой точкой. Зависимость величины скорости фильтрации и напора только от одной координаты – от радиуса вектора точки – позволяет провести полное исследование плоскорадиального потока столь же элементарными методами, как и в случае одномерного потока.
Третий тип Если все частицы жидкости (или газа) движутся в пористой среде так, что их скорости фильтрации не параллельно одной и той же плоскости, то такое движение называется пространственным, или трёхмерным, ибо для определения положения частицы жидкости в пространстве требуются три координаты. Если при пространственном движении все траектории прямолинейны и радиально сходятся в одной точке (или расходятся из одной точки), то такое движение называется трёхмерным радиальным, или сферическим радиальным.
Геометрия фильтрационных потоков нефти, газа и воды в реальных пластах может быть очень сложной: границы водонефтяного или водогазового контактов бывают самой причудливой формы, пласты часто имеют переменную по простиранию толщину, месторождения разрабатываются десятками и сотнями скважин, которые могут вскрывать пласт не на всю его толщину (так называемые несовершенные по степени вскрытия скважины), и т.д. все это усложняет картину фильтрации и с трудом поддается учету. Вот почему при изучении реальных явлений, происходящих в пластах, необходимо предварительно рассмотреть простейшие фильтрационные потоки. Из которых, как из элементов, затем можно составить модели более сложных явлений.
Параллельно – прямолинейная фильтрация. Рассмотрим случай фильтрации жидкости в прямолинейном пласте (рисунке 4.1. ).

Пусть имеется пласт в форме параллелепипеда длиною L, шириною (в плане) В и толщиною h с непроницаемыми кровлей и подошвой (например, с расположенными выше и ниже него глинистыми пластами). На левой границе пласта, принимаемой за контур питания[3], давление рк, на правой, называемой галереей1,- рr. Этим давлениям соответствуют напоры Нк и Нr . так как площадь фильтрации ( s = Bh ) постоянна по длине пласта, линии тока жидкости будут параллельны друг другу, а поля скоростей и приведенных давлений для любого горизонтального параллельного линиям тока сечения пласта будут одинаковыми ( поперечных перетоков жидкости в нем нет). Такую фильтрацию называют прямолинейно-параллельной. Она происходила в опытах Дарси. (Напомним, что приведенные давления не зависят от положения пласта в пространстве).
Следовательно, расход (называемый дебитом) галереи по формуле (4,1)
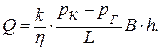 (4,1)
(4,1)
Скорость фильтрации, одинаковая для любого живого сечения пласта, определяется по выражению
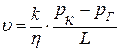 . (4,2)
. (4,2)
Возьмем параллельное галерее произвольное живое сечение пласта, отстоящее от нее на расстоянии х, давление в котором равно p, а напор Нх . приняв его за контур питания, запишем закон Дарси и выразим из него р:
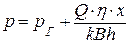
 (4,3)
(4,3)
Подставив в это выражение значение Q из закона Дарси, получим закон распределения давления по длине пласта:
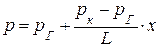 (4,4)
(4,4)
Линия падения давлений, следовательно, и соответствующих им напоров Н = р/ ( рg ) представляет собой прямую ( рисунок 4.1).
При разработке нефтяных месторождений примером фильтрации, близкой к прямолинейно-параллельной, служит фильтрация в полосовой залежи, эксплуатирующейся прямолинейной цепочкой скважин (рисунок 4.2).

До некоторого сечения А – А линии тока жидкости будут практически параллельными, а их искривление начнется вблизи от скважин (рис. 2). Чем больше скважин в батарее, тем ближе к ней сечение А – А. При бесконечном их числе батарея превратиться в галерею.
Плоскорадиальная фильтрация. Рассмотрим другой простейший случай фильтрационного потока – плоскорадиальную фильтрацию несжимаемой жидкости. Пусть скважина расположена в центре кругового пласта толщиной h (рисунок 4.3.).
| |  |
Рисунок 4.3. Плоскорадиальная фильтрация жидкости.
Обозначим радиус контура питания RK , радиус скважины rc, давление на них соответственно рк и рс. Пока скважина не эксплуатируется, в любой точке пласта давление рк , а соответствующий ему статистический уровень Нк = рк / ( рg ). Для того чтобы жидкость притекала к скважине, необходимо снизить давление на ее забое ( нижней точке) рс,, т.е. создать условие рк > рс ( или Нк > Нс, где Нс = рс / ( рg ) – динамический уровень жидкости в скважине). Если при этом динамический уровень окажется больше глубины скважины, она будет фонтанировать, т.е. жидкость сможет поступать на поверхность земли только за счет затрат пластовой энергии ( гидростатического напора). Если Нс меньше глубины скважины ( см. рис.3), добывать жидкость можно только за счет внешних источников энергии (например, насосами). Линии тока жидкости в рассматриваемом случае направлены от контура питания к скважине по радиусу пласта, а поля скоростей фильтрации и давлений для любого его горизонтального сечения одинаковы. Такую фильтрацию называют плоскорадиальной.
Мысленно выделим элементарную струйку жидкости вдоль радиуса пласта ( на плане рисунке 4.3. эта струйка заштрихована ). Так как поперечные размеры струйки малы, движение в ней можно считать параллельно-прямолинейным. На бесконечно малом перемещении dr падение давления вдоль струйки будет dp. Подставив в выражение (4.4 ) вместо длины перемещения l величину dr, а вместо падения давления Dр величину dp, получим закон Дарси в дифференциальной форме:
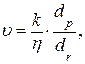 (4.5.)
(4.5.)
| где | dp/ dr | - | градиент давления. |
Скорость фильтрации υ и давление р для точек пласта, отстоящих на одинаковых расстояниях r от его центра, в силу симметрии будут одинаковыми. Объемный расход жидкости через произвольное живое сечение пласта s (r) ( в виде боковой поверхности цилиндра радиусом r и высотой h )
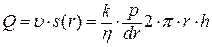 (4,6)
(4,6)
Разделив переменные и подставив пределы интегрирования для р от рс до рк , а для r от rc до Rk , получим:
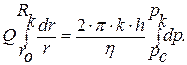 ( 4,7)
( 4,7)
После интегрирования
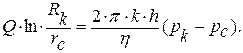 (4,8)
(4,8)
Решив последнее выражение относительно Q, окончательно имеем
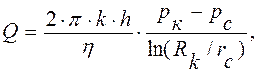 (4,9)
(4,9)
где разность давлений рк - рс называют депрессией. Выражение (4.9.), являющееся законом Дарси для плоскорадиальной фильтрации, называют формулой Дюпюи, которая считается основной при расчетах, связанных с эксплуатацией нефтяных месторождений, а также водяных артезианских скважин.
В формуле (4,9.) значение Rk находится под логарифмом, поэтому ошибка в его определении незначительно сказывается на дебете. Обычно за Rk (если скважина одна) принимают расстояние от скважины до границы водонефтяного контакта, а если пласт разрабатывается большим числом скважин, то за Rk принимают половину расстояния между ними.
Приняв за Rk произвольный радиус r , а за рк соответствующее этому радиусу давление в пласте р, разрешим формулу Дюпюи относительно р:
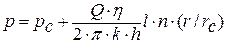 (4,10)
(4,10)
Заменив в этом выражении Q на полученное из выражения (4.9.), имеем:
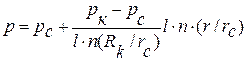 (4,11)
(4,11)
Из уравнения (4.11) видно, что закон распределения давлений ( а, следовательно, и динамических напоров) при плоско-радиальной фильтрации логарифмический. Поверхность, образующуюся от вращения логарифмической пьезометрической линии, соединяющей динамические уровни, называют воронкой депрессии (рисунок 4.3.).
Из анализа формулы (4.11.) или рассмотрения воронки депрессии видно, что наибольшие потери давления ( или соответствующие им потери напора) происходят вблизи от скважины ( в призабойной зоне).
В промысловых условиях для повышения дебита скважин проницаемость призабойной зоны стремятся увеличить. Для этого проводят гидравлические разрывы пласта, обработку такой зоны кислотой ( если пласт состоит из карбонатных пород) и другие технологические операции, облегчающие приток нефти или газа к скважинам.
По формуле (4.11.) можно определить давление р в любой точке пласта, отстоящей от скважины на произвольном расстоянии r.
4.2.Неустановившееся движение жидкости и газа в пористой среде.
При неустановившемся движении скорость в каждой данной точке пространства изменяется с течением времени, т.е. в общем случае получим следующее:
Частица М, придя в любую точку пространства, имеет в этой точке в момент времени t скорость V.
Частица М2 придя в ту же точку пространства в другой момент времени t, имеет в этой точке другую скорость V2 и т. д.
Следовательно, при неустановившемся движении
V = f (x, y, z, t)
В качестве примера неустановившегося движения жидкости в пористой среде рассмотрим неустановившуюся одномерную фильтрацию сжимаемой жидкости.
Пусть пласт вскрыт не скважиной, а прямолинейной галереей. Модель пласта представлена на рисунке 4.4.

Рисунок 4.4. Горизонтальное сечение элемента пласта в условиях
одномерного потока.
При отборе жидкости, галлереи давление в ней будет меньше первоначального давления Рк. Вследствие этого в пласте начнётся первая фаза неустановившейся фильтрации жидкости, сущность которой рассмотрена в главе 2 (безнапорное движение жидкости в колодце).
Задачу в первой фазе неустановившейся одномерной фильтрации сжимаемой жидкости следует рассматривать в двух случаях.
Первый случай – это случай, когда дебит галлереи является постоянным.
В этом случае время t, истёкшее с начала отбора жидкости из галлереи, падение давления распространилось на расстояние xк от галлереи. Тогда масса жидкости, извлечённой из пласта за это время, равна Qмt, где Qмconst. С другой стороны, масса извлечённой из пласта жидкости ровна изменению массы жидкости, находящейся в пласте.
Следовательно можно записать уравнение
Qм t = Vn (  к-
к- 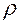 ), ( 4.12 )
), ( 4.12 )
| где Vп | - объём парового пространства области пласта. |
Vn=mFxк (4.13.)
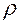 к к
| - плотность жидкости в точках пласта, для которых координата х≥ хк |
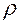 к = const
к = const
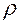
| - средневзвешенная по объёму Vn плотности жидкости, которая в условиях одномерного движения выражается в виде: |
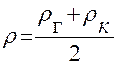 ,
,  (4.14.)
(4.14.)
где 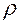 г г
| - плотность жидкости у входа в галлерею |
Подставляя в уравнение (4.12 ) вместо Qм Q и 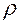 их значения получим
их значения получим
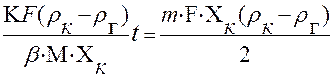 , (4.15.)
, (4.15.)
здесь
| F | - площадь вертикального сечения пласта; |
| β | - коэффициент объёмного упругого расширения жидкости; |
| К | - коэффициент фильтрации; |
| М | - обсалютная динамическая вязкость. |
Из формулы ( 4.15.) получим
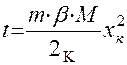 ; (4.16.)
; (4.16.)
откуда
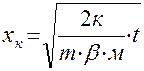 (4.17.)
(4.17.)
зная величину ХК, легко найти давление в галерее 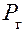 .
.
Объёмный расход жидкости равен
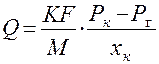 (4.18.)
(4.18.)
следовательно
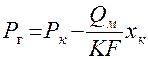 (4.19.)
(4.19.)
Второй случай – это случай, когда в галерее поддерживается постоянное противодавление.
В указанном случае уравнение материального баланса даётся формулой
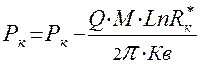 , (4.20.)
, (4.20.)
| где Q | - Объёмный расход жидкости |
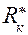
| - безразмерный радиус |
| в | - мощность пласта. |
Подставляя в уравнение значения Qм,, Vп и 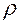
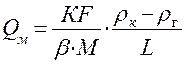 , (4.21.)
, (4.21.)
Vп=mFхк (4.22.)
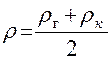 (4.23.)
(4.23.)
и учитывая, что при Рг= const
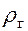 = const, имеем:
= const, имеем:
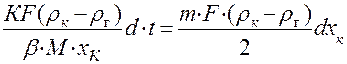 (4.24.)
(4.24.)
откуда
dt= 
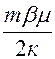 xкdxк
xкdxк  (4.25.)
(4.25.)
Интегрируя полученное уравнение по xк в пределах от 0 до xк и по t от 0 до t, находим:
t= 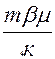 x
x 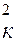 (4.26.)
(4.26.)
что дает
xк= 2 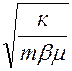 t (4.27.)
t (4.27.)
Подставляя значение xк из формулы (4.27.) в формулу (4.21.) найдем изменение во времени объемного расхода жидкости (дебит галлереи).
Как видно из формул ( 4.17) и ( 4.27.), в рассмотренных условиях однокамерного движения расстояние xк от галлереи до границы области падения давления в пласте пропорционально корню квадратному из времени t.
Определим массу жидкости QДМ, извлеченной из пласта к моменту времени Т, когда область падения давления распространится до контура питания пласта, расстояние до которого обозначим Lк.
QДМ= 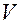 кП (
кП ( 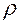 к-
к- 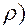 , (4.28)
, (4.28)
где VКП=mFLк.
или
QДМ= 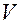 кП (
кП ( 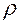 к-
к- 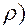 =mFLк(
=mFLк( 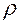 к-
к- 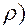 (4.29.)
(4.29.)
Подставляя вместо 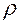 его значение из формулы ( 4.23.) получим
его значение из формулы ( 4.23.) получим
Q= 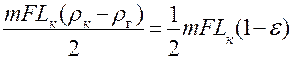 , (4.30)
, (4.30)
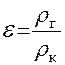
Но согласно формулы
1-ε  β(Рк - Рг) , (4.31.)
β(Рк - Рг) , (4.31.)
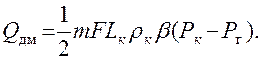 (4.32.)
(4.32.)
Разделить Qдм на плотность жидкости 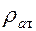 при атмосферном давлении и принимая
при атмосферном давлении и принимая 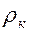 /
/ 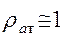 , получим объём жидкости Qдоб, извлечённой за время Т:
, получим объём жидкости Qдоб, извлечённой за время Т:
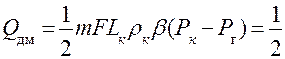 VКПβ(Рк-Рг) (4.33.)
VКПβ(Рк-Рг) (4.33.)
Как видно из формулы ( 4.33.), этот объём жидкости прямо пропорционален объёму порового пространства пласта VКП, коэффициенту объемного упругого расширения жидкости β и величине депрессии (РК-РГ).
Дата добавления: 2016-02-16; просмотров: 3698;
