В нефтегазовых пластах
Традиционный подход к расчету разработки и эксплуатации нефтяных и газовых залежей основывается на теории фильтрации. Система уравнений фильтрации включает в себя закон фильтрации, уравнения неразрывности (для простоты ниже рассматривается случай изометрической фильтрации), которые записываются в локальных переменных. Для однозначного определения полей давления и скоростей фильтрации система уравнений дополняется начальными и граничными условиями, причем последние определяются давлением или скоростью фильтрации (или их комбинацией) на контуре пласта и скважин. Такой подход подразумевает, что условия на скважинах, точнее на забое скважин, известны или реализуются по заранее заданной программе. Вообще говоря, такое допущение, как правило, не выполняется. Режим работы скважин, то есть ее дебит и забойное давление, устанавливается в результате взаимодействия скважин, а также условий в системе «пласт - скважина - наземное оборудование». Если оборудовать данную технологическую цепочку, то можно принять известным или заданным давление на выходе из скважин. Вполне возможно, что взаимодействие скважин через наземное оборудование не менее существенно, чем через пласт. Однако учет фактора сильно усложняет рассмотрения. Таким образом, при моделировании процесса эксплуатации залежи необходимо учитывать как работу самого пласта, так и влияние скважин, а также их взаимодействие. Необходимость такого учета обусловлена тем, что инерциальность и емкость системы скважин соизмерена с пластовым, а основные сопротивления сосредоточены в непосредственной окрестности скважин (призабойной зоне). В дальнейшем под скважиной понимается совокупность призабойной зоны и собственно скважины. Влияние скважины на происхождение в пласте процессы является ощутимым, и при рассмотрении и фильтрации необходимо учитывать работу собственно скважины.
Влияние скважин на происходящие в пласте процессы является ощутимым, и при рассмотрении и фильтрации необходимо учитывать работу собственно скважин.
В принципе это можно учесть, если рассматривать совместно работу пласта и скважин. При этом следует выписать уравнения фильтрации и уравнения движения жидкости в стволе скважин, использовать условия «смешивания» решения для пласта и каждой скважины на каждом контуре скважины, а также задать граничные и начальные условия в пласте и на устье скважины. Однако при таком подходе результаты расчетов становятся труднообозримыми, не говоря уже о трудностях счета, поскольку количество скважин на залежи достигает сотен и тысяч единиц. Учитывая это обстоятельство, целесообразно использовать иной подход, предполагающий замену скважин-стоков конечных размеров непрерывным по площади распределением отборов. При этом реальная система «пласт-скважина» моделируется сплошной двойной средой, состоящей собственно из пористой среды и среды «скважин».
Рассмотрим одномерный нестационарный случай.
Система уравнений включает:
закон фильтрации
F1 (px, Q, pxt, Qt …) = 0; (3.1)
уравнение неразрывности

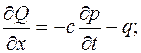 (3.2)
(3.2)
уравнение движения в скважинах
F2 (q ,p, qt, pt…) = 0 , (3.3)
где p, Q – давление и расход жидкости;
с – упругоемкость пласта; 
q – распределительный отток жидкости из пласта в скважины.
Ограничиваясь линейным случаем, получим уравнение движения в скважине (3.3.). Если не учитывать постоянное несущественное слагаемое за счет гидростатистического давления и принять, что давление на устьях скважин постоянно (это давление принимается за нулевой уровень), то уравнение баланса количества движения можно записать в виде
p = α qt + βq + γò (q – q1) dt, (3.4.)
где q, q1 - распределенные расходы жидкости из пласта в скважину и из скважины в сборную систему. Первое слагаемое в правой части уравнения (3.4.) соответствует перепаду давления за счет ускорения жидкости в скважине, второе – потерям на трение, третье – изменению давления за счет накопления жидкости в скважине. Положим, что q1 = d,p. Это соответствет тому, что расход жидкости из скважины определяется только потерями на выходе из скважины (штуцере). Тогда из (3.4.) получаем:
α qtt + βqt + γ qt = pt + γ d р (3.5.)
Исходя из управлений (3.1), (3.2), (3.5), легко получить одно уравнение для p или Q. Конкретизируем с этой целью вид закона фильтрации. Предположим, что жидкость обладает релаксационными свойствами. В этом случае уравнение (3.1) может быть записано, например в одном из двух видов:
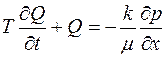
(3.6)
или
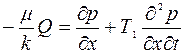
(3.7)
Используем в начале закон фильтрации (3.6). Исключая из уравнений (3.6), (3.2), (3.5) Q, получаем уравнение для p:
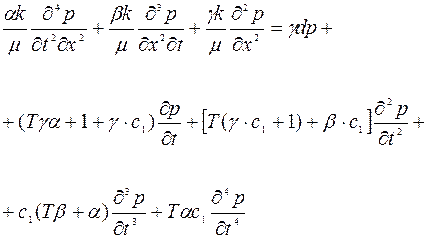
(3.8)
Уравнение (3.8) значительно сложнее обычного уравнения пьезопроводности . Если скважина закрывается на забое, то ее емкость обращается в нуль, а сопротивление становится бесконечно большим. Поэтому в уравнение (3.8) следует положить α=0, γ=∞. В этом случае уравнение (3.8) принимает вид, характерный для фильтрации с релаксацией:
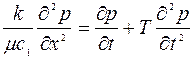 (3.9)
(3.9)
Если жидкость релаксаций не обладает (Т=0), то уравнение (3.9) превращается в обычное уравнение пьезопроводности. Такая ситуация является типичной при снятии кривой восстановления давления (КВД). Известно, что по КВД определяют как расчетную модель в пласте, то есть вид уравнения фильтрации, так и параметры модели. Сравнение уравнений (3.8) и (3.9) показывает, что выключение скважин означает изменение структуры системы, и в измененном виде система описывается уравнением (3.9) или уравнением пьезопроводности. Отсюда следует, что при остановке скважины по КВД нельзя определить модель и ее параметры, а фактически определяются параметры измененной системы.
Рассмотрим теперь ту же систему, однако скважины закрываются теперь на устье. В этом случае q1=0, то есть величина d в уравнении (3.5) равна нулю. Уравнение фильтрации принимает соответственно вид (3.8), где положено d=0:
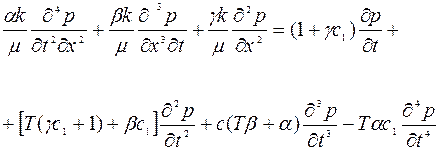 (3.10)
(3.10)
Очевидно, что уравнения (3.8) и (3.10) отличаются ( с точностью до коэффициентов) только слагаемым γdp. Нетрудно проверить, что если пренебречь распределенным сопротивлением пласта по сравнению с сопротивлением скважины и призабойной зоны, то есть вместо (3.6) использовать
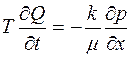 (3.11)
(3.11)
то получается уравнение, аналогичное (3.8).
Ясно, что уравнения (3.8) и (3.10) описывают работу пласта с учетом взаимодействия скважин. Важным является то обстоятельство, что это взаимодействие обусловлено как наличием связи между скважинами через пласт, которое в рамках традиционного описания называется интерференцией, так и внутренними параметрами скважин (α, β, γ). Поэтому в действительности взаимодействие между скважинами носит более сложный характер, чем просто интерференция.
Математически это отражено структурой уравнений (3.8) и (3.10), которые существенно отличаются от уравнения пьезопроводности, на основе которого обычно изучается интерференция. Важно также отметить, что даже не работающие, закрытые на устье скважины, являясь, в сущности, аналогом колебательного контура (уравнение (3.5)), в значительной степени влияют на поле давлений в пласте. При выводе предыдущих уравнений предполагалось, что устьевое давление на скважинах поддерживалось постоянным. Если устьевое давление скважин неодинаково (переменность по координате) или меняется во времени, то это приводит к появлению в (3.8) или (3.10) неоднородного слагаемого, не влияющего на качественный характер решения.
Если закон фильтрации имеет вид (3.7), то соответствующее уравнение записывается в форме
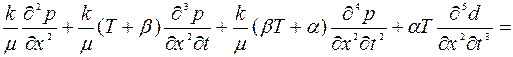
= γαr+ (1 + γс1 ) 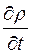 + br1
+ br1 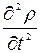 + 2с1
+ 2с1 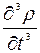 (3.12)
(3.12)
Рассмотрим далее влияние нелинейностей. Будем считать, что с1=с1( 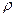 ). Это означает, что коэффициент упругоемкости зависит от давления, что характерно, например, для газированных жидкостей или трещиноватых сред. Рассмотрим случай, когда скважины закрыты на устье. В этих условиях в (3.5) следует положить d=0. введем явно малый параметр
). Это означает, что коэффициент упругоемкости зависит от давления, что характерно, например, для газированных жидкостей или трещиноватых сред. Рассмотрим случай, когда скважины закрыты на устье. В этих условиях в (3.5) следует положить d=0. введем явно малый параметр 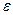 , положив
, положив 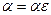 ,
, 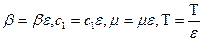 . Уравнение (3.5) можно переписать в виде
. Уравнение (3.5) можно переписать в виде
 q =
q = 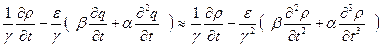 . (3.13)
. (3.13)
Подставляя (3.13) в (3.12), находим
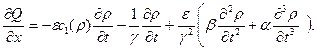 (3.14)
(3.14)
Уравнение перепишется в виде:
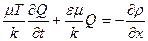 . (3.15)
. (3.15)
При ε « 1 можно искать решение в виде простой волны, в которой ρ и Q связаны, как в линейной системе Q = 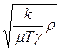 .
.
Тогда вместо (3.14) получаем
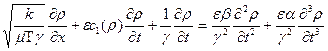
Учитывая, что в простой волне 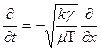 , вместо последнего уравнения получаем
, вместо последнего уравнения получаем
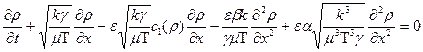
Переходя к движущейся системе координат t = t, 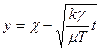 , получаем уравнение Бюргерса – Кортвега – де Фриза
, получаем уравнение Бюргерса – Кортвега – де Фриза
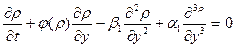
 , (3.16)
, (3.16)
где
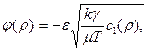
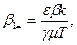
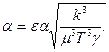
Уравнения типа (3.16) могут быть получены и для других условий. Будем считать справедливым условие t « (γα)-1, то есть рассматриваются быстропротекающие процессы. Тогда вместо (3.5) вновь справедливо (3.13). Будем считать, что фильтрация описывается законом Дарси Q = - 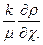 Используя это соотношение, а также (3.13) и (3.2), получаем с учетом α = α ε, β = β ε, с1 = с1 ε
Используя это соотношение, а также (3.13) и (3.2), получаем с учетом α = α ε, β = β ε, с1 = с1 ε
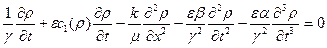 (3.17)
(3.17)
Будем искать решение уравнения (3.17) в виде волны, двигающейся вправо, то есть используем соотношение 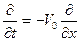 . Тогда вместо (3.17) получаем
. Тогда вместо (3.17) получаем
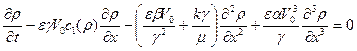 (3.18)
(3.18)
Пусть теперь справедлив закон фильтрации. Тогда вместо (3.17) будем иметь
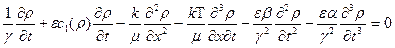
Ищем решение этого уравнения в виде волны, для чего полагаем
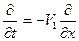 . Имеем:
. Имеем:
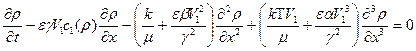 (3.19)
(3.19)
Уравнения (3.16), (3.18), (3.19) являются уравнениями Бюргерса – Кортвега – де Фриза и описывают волновой процесс. Таким образом, наличие скважин приводит к тому, что характер фильтрационных процессов оказывается иным, чем при обычном рассмотрении, учитывающим только свойства пласта и жидкости. Как это уже отмечалось, взаимодействие между скважинами определяется как свойствами пластовой системы, так и собственными параметрами скважин. В зависимости от соотношения между определяющими параметрами характер волновых процессов в пласте может быть различным. Так, например, как это следует из общих свойств уравнения БКФ, возможны режимы монотонной и осциллирующей волны. Это делает возможным осуществление различных технологических операций, основанных на взаимодействии скважин. Например, реализация режима осциллирующей волны соответствует операции барообработки нефти или изменению свойств коллектора.
Произведем оценку точности модели, ограничиваясь стационарным случаем. В этих условиях вместо, например, уравнения (3.8) получаем
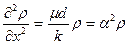
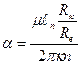 (3.20)
(3.20)
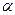 - величина обратная коэффициенту продуктивной скважины
- величина обратная коэффициенту продуктивной скважины
Рассмотрим (в безразмерных переменных) задачу определения дебита прямолинейной галереи, находящейся в сечении 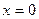 при забойном давлении
при забойном давлении 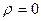 , давление на контуре питания при
, давление на контуре питания при 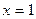
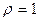 . В обычной постановке следует искать решение уравнения
. В обычной постановке следует искать решение уравнения 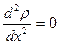 при условиях
при условиях 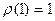 ,
, 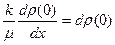
Последнее соотношение представляет собой равенство расходов из пласта и в скважине. Решение данной задачи имеет вид 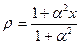 , откуда расход при х=0 равен:
, откуда расход при х=0 равен:
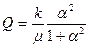 (3.21)
(3.21)
В случае «равномерно распределенной скважины» решение уравнения (3.20) ищется при условиях 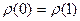 и имеет вид:
и имеет вид:
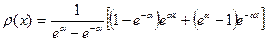
Общий расход Q равен
Q1=d 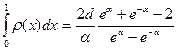
Точность модели может быть оценена отношением 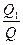
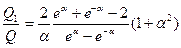
Поскольку d« 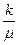 - основные сопротивления сосредоточены вблизи скважины, то отношение
- основные сопротивления сосредоточены вблизи скважины, то отношение 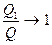 при
при 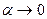 . При
. При 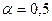
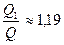 . Рассмотрим теперь радикальный случай. Уравнение (3.8) превращается в данном случае в уравнение Бесселя.
. Рассмотрим теперь радикальный случай. Уравнение (3.8) превращается в данном случае в уравнение Бесселя.
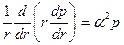 (3.22)
(3.22)
Пусть скважина радиуса p расположена в центре кругового пласта радиуса R=1, на контуре которого p=1, давление на скважине p=0. Дебит такой скважины на единицу мощности пласта равен
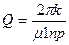
При анализе распределенной системы следует решать уравнение (3.22) при условиях p(1)=0, p(0)≠∞. Чтобы избежать громоздких выкладок, заменим уравнение Бесселя (3.22) на
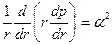 (3.23)
(3.23)
для чего заменим p в правой части (3.22) на его максимальное значение, равное единице. В силу теоремы сравнения для обыкновенных дифференциальных уравнений решение уравнения (3.23) является оценкой снизу для решения (3.22). решение (3.23) при сформулированных условиях находим
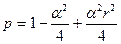
Расход определится из соотношения
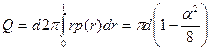
В радиальном случае за величину d можно принять
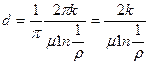
Тогда отношение 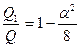 и
и 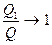 при
при 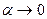 .
.
При 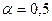 ,
, 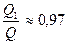 .
.
Дата добавления: 2016-02-16; просмотров: 1248;
