Правила образования языка в алфавите (синтаксис языка).
Для описания правил введем понятие метасимвол. Метасимвол – это не принадлежащее языку обозначение, которое позволяет вводить понятия и свойства этого языка, а также указать порядок, в котором должны применяться правила языка.
Введем 4 метасимвола для иллюстрации заданных правил примерами:
1) x 2) y 3) ( 4) ) . Метасимволы x и y будут служить для обозначения формул, а скобки ( и ) – для указания порядка применения правил.
Правила образования языка в алфавите следующие:
Базисное правило: всякое высказывание есть формула.
 Правило индукционного шага: если x и y – формулы, то
Правило индукционного шага: если x и y – формулы, то 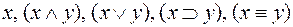 - тоже формулы.
- тоже формулы.
Правило ограничения: формулы могут образовываться только по правилам 1 и 2 .
Других правил нет.
Как же метасимволы скобок указывают на порядок применения правил? Рассмотрим пример.
 Пусть, х (p/\(q\/r)). При построении формулы х правило индукционного шага применялось дважды: первый раз – при построении формулы (q\/r) из формулы q и r, а второй – при построении заключительной формулы из формул p и (q\/r). Указанные правила образования языка в алфавите используются для представления составных сколь угодно сложных высказываний.
Пусть, х (p/\(q\/r)). При построении формулы х правило индукционного шага применялось дважды: первый раз – при построении формулы (q\/r) из формулы q и r, а второй – при построении заключительной формулы из формул p и (q\/r). Указанные правила образования языка в алфавите используются для представления составных сколь угодно сложных высказываний.
Формулы языка делятся на атомы или атомарные формулы и формулы (без эпитетов), к которым относятся все составные формулы, т.е. формулы, образованные с помощью связок, а атомы – это неделимые (исходные) высказывания.
3.2.3. Правила присвоения истинностных значений формулам
(семантика языка)
По определению атом может иметь только два значения: либо ‘‘истина‘‘ (И) либо ‘‘ложь‘‘ (Л). Каждое из этих значений называют истинностным. Правила присвоения истинностных значений формулам 5-ти связок представлены в табл. 3.2.
Таблица 3.2
 x x
| y | x | x Ù y | x Ú y | x É y | x º y |
| И | И | Л | И | И | И | И |
| И | Л | Л | Л | И | Л | Л |
| Л | И | И | Л | И | И | Л |
| Л | Л | И | Л | Л | И | И |
Введем ряд новых понятий, которые понадобятся при рассмотрении следующих аспектов исчисления высказываний.
1) «Интерпретировать формулу» - приписать ей одно из двухзначений истинности И или Л.
2) «интерпретация для формулы» - это набор истинностных значений всех атомов, входящих в формулу, предназначенный для одновременной замены ими самих атомов в этой формуле. Формула, содержащая К различных высказываний, допускает 2к интерпретаций.
Проиллюстрируем эти два понятия на примерах интерпретации некоторых формул (табл. 3.3):
Таблица 3.3
 x y z x y z
| y É z | x É(yÉz) | x Ù y | (x Ù y)Éz | w | w |
| И И И | Л | И | И | И | И | Л |
| И И Л | Л | Л | И | Л | И | Л |
| И Л И | И | И | Л | И | И | Л |
| И Л Л | И | И | Л | И | И | Л |
| Л И И | И | И | Л | И | И | Л |
| Л И Л | Л | И | Л | И | И | Л |
| Л Л И | И | И | Л | И | И | Л |
| Л Л Л | И | И | Л | И | И | Л |
Первые три столбца каждой строки являются одной из возможных интерпретаций.
3) семантика языка -это полный набор правил интерпретации формул. Это вся таблица 3.2.
4) «Общезначимость формулы» -это истинность формулы при всех возможных её интерпретациях. ( w в табл. 3.3)
5) 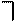
 «противоречивость формулы» (невыполнимость) - это ложность формулы при всех возможных её интерпретациях ( w в табл.3.3)
«противоречивость формулы» (невыполнимость) - это ложность формулы при всех возможных её интерпретациях ( w в табл.3.3)
6) «эквивалентность формул» - формулы x и y эквивалентны, когда истинностные значения x и y совпадают при каждой общей интерпретации для x и.
7) «Литера» -это атом или его отрицание.
8) «дизъюнкция формул» - это формула X , образованная из исходных формул F1,F2,...,Fn с помощью дизъюнктивной (и только) связки:
X = F1  F2
F2  ,...
,...  Fn.
Fn.
9) «Конъюнкция формул»-это формула Y, образованная из исходных формул F1,F2,...,Fn с помощью конъюнктивной (и только) связки:
Y = F1 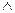 F2
F2 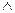 ,...
,... 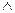 Fn.
Fn.
10) «Дизъюнкт»- это формула Z, образованная из исходных литер (и только литер) с помощью дизъюнктивной (и только) связки:
Z = A1  A2
A2  A3
A3  ,...
,...  An.
An.
Эквивалентом дизъюнкта является множество входящих в него литер:

 Z = A1
Z = A1  A2
A2  ,...
,...  Am
Am  {A1 , A2 ,..., Am}
{A1 , A2 ,..., Am}
11) «R - литерный дизъюнкт» - это дизъюнкт, в котором Rлитер.
12) «Единичный дизъюнкт» - это дизъюнкт с одной литерой.
13) «Пустой дизъюнкт»- это дизъюнкт, в котором нет литер. Т.к. он не содержит литер, которые могли бы быть истинными при некоторой интерпретации, он всегда ложен
14)  «Область действия логических связок» - при бесскобочной записи эта область упорядочена по убыванию и соответствует последовательности º , É , Ù , Ú , .
«Область действия логических связок» - при бесскобочной записи эта область упорядочена по убыванию и соответствует последовательности º , É , Ù , Ú , .
15) Дизъюнктивная нормальная форма» - это формула
F= F1  F2
F2  ,...
,...  Fn , где Fi - конъюнкция литер.
Fn , где Fi - конъюнкция литер.
16) Конъюнктивная нормальная форма» -
F=F1 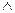 F2
F2 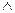 ,...
,...  Fn , где Fi - дизъюнкция литер.
Fn , где Fi - дизъюнкция литер.
17) «Выполнимая формула» - формула выполнима тогда и только тогда, когда существует, по крайней мере, одна интерпретация, при которой эта формула истинна. Эта интерпретация называется моделью формулы.
18)  «Контрарная пара формул» - это множество { A , A}
«Контрарная пара формул» - это множество { A , A}
19) «Тавтология» - общезначимая формула, истинная во всехеё интерпретациях. Дизъюнкт, содержащий контрарную пару, является тавтологией.
20) «Приведенная КНФ»- это КНФ, из которой удалены тавтологии и повторения литер в пределах одного итого же дизъюнкта. Вернуться
3.2.4. Правила вывода в исчислении высказываний(стереотипы
Дата добавления: 2016-03-27; просмотров: 706;
