Продукционные модели

В моделях этого типа используются некоторые элементы логических и сетевых моделей. Из логических моделей заимствована идея правил вывода, которые здесь называются продукциями, а из сетевых моделей – описание знаний в виде семантической сети. В результате применения правил вывода к фрагментам сетевого описания происходит трансформация семантической сети за счет смены её фрагментов, наращивания сети и исключения из неё ненужных фрагментов. Таким образом, в продукционных моделях процедурная информация явно выделена и описывается иными средствами, чем декларативная информация. Вместо логического вывода, характерного для логических моделей, в продукционных моделях появляется вывод на знаниях.

Продукции, с одной стороны, близки к логическим моделям, что позволяет организовать на них эффективные процедуры вывода, а с другой стороны, более наглядно отражать знания, чем классические логические модели. В них отсутствуют жесткие ограничения, характерные для логических исчислений, что дает возможность изменять интерпретацию элементов продукции.

В общем виде под продукцией понимается выражение следующего вида:

( i ) ; Q ; P ; A ðB ; N .

Здесь i – имя продукции, с помощью которой данная продукция выделяется из всего множества продукций. В качестве имени может выступать некоторая лексема, отражающая суть данной продукции (например, «покупка книги», набор кода замка), или порядковый номер продукции в их множестве, хранящемся в памяти системы.

Элемент Q характеризует сферу применения продукции. Такие сферы легко выделяются в когнитивных структурах человека. Наши знания как бы ‘‘разложены по полочкам‘‘. На одной ‘‘полочке‘‘ хранятся знания о том, как надо готовить пищу, на другой – как добраться до работы и т. п. Разделение знаний на отдельные сферы позволяет экономить время на поиск нужных знаний. Такое же разделение на сферы в базе знаний интеллектуальной системы целесообразно и при использовании для представления знаний продукционных моделей.

Основным элементом продукции является её ядро: АðВ. интерпретация ядра продукции может быть различной и зависит от того, что стоит слева и справа от знака секвенции ð. Обычное прочтение ядра продукции выглядит так: ЕСЛИ А, ТО В, более сложные конструкции ядра допускают в правой части альтернативный выбор, например, ЕСЛИ А, ТО В₁, ИНАЧЕ В_2.

Секвенция может истолковываться в обычном логическом смысле как знак логического следования В из истинного А (если А не является истинным выражением, то В ничего сказать нельзя). Возможны и другие интерпретации ядра продукции, например, А описывает некоторое условие, необходимое для того, чтобы можно было совершить действие В.

Элемент Р есть условие применимости ядра продукции. Обычно Р представляет собой логическое выражение (как правило, предикат). Когда Р принимает значение «истина», ядро продукции активизируется. Если Р ложно, то ядро продукции не может быть использовано. Например, если в продукции: «наличие денег; если хочешь купить вещь Х, то заплати в кассу её стоимость и отдай чек продавцу», условие применимости ядра ложно, т.е. если денег нет, то применить ядро продукции невозможно.

Элемент N описывает постусловия продукции. Они актуализируются только в том случае, если ядро продукции реализовалось. Постусловия продукции описывают действия и процедуры, которые необходимо выполнить после реализации ядра. Например, после покупки некоторой вещи в магазине необходимо в описи товаров, имеющихся в этом магазине, уменьшить количество вещей такого типа на единицу. Выполнение N может происходить не сразу после реализации ядра продукции.

Если в памяти системы хранится некоторый набор продукций, то они образуют систему продукций. В системе продукций должны быть заданы специальные процедуры управления продукциями, с помощью которых происходит актуализация продукций и выбор для выполнения той или иной продукции.

Базовая структура продукционной системы состоит из трех основных компонентов [10]. Первый из них – это набор правил, используемый как база знаний, поэтому его еще называют базой правил. Вторым компонентом является рабочая память (или память для кратковременного хранения), в которой хранятся предпосылки, касающиеся конкретных задач предметной области, и результаты выводов, полученные на их основании. Третий компонент - это механизм логического вывода, использующий правила в соответствии с содержимым рабочей памяти (рис.2.8).

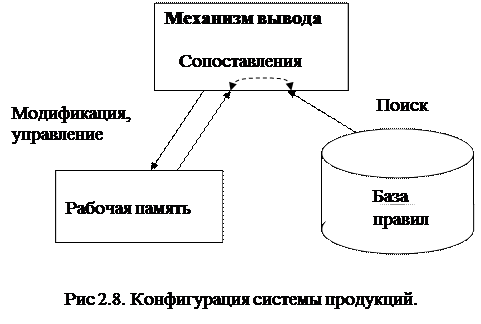Для того чтобы показать, как взаимодействуют эти элементы, рассмотрим несложный пример. Данные, записываемые в рабочую память, представляют собой образцы в виде набора символов, например, «намерение – отдых», «место отдыха – горы» и т.п. Правила, записываемые в базу правил, отражают содержимое рабочей памяти. В их условной части находятся либо одиночные образцы, либо несколько условий, соединенных предлогом «и», а в заключительной части – образцы, дополнительно регистрируемые в рабочей памяти. Пусть, например, правила таковы:

Правило 1. ЕСЛИ «намерение – отдых» и

«дорога ухабистая» ТО «использовать джип»

Правило 2. ЕСЛИ «место отдыха – горы» ТО «дорога ухабистая»

После того как в рабочую память записываются образцы «намерение – отдых» и «место отдыха – горы», рассматривается возможность применения этих правил. Известны два подхода для получения логического вывода системы – прямой вывод и обратный вывод. Рассмотрим суть этих подходов.

При прямом выводе совершается работа по извлечению предварительно записанного содержимого рабочей памяти, применению правил и дополнения данных, помещаемых в память. Сначала механизм вывода сопоставляет образцы в условной части с образцами, хранимыми в рабочей памяти. Если все образцы имеются в рабочей памяти, то условная часть считается истинной, в противном случае - ложной. В данном примере образец «намерение – отдых» существует в рабочей памяти, а образец «дорога ухабистая» отсутствует, поэтому условная часть правила 1 считается ложной. Условная часть правила 2 является истинной. Поскольку в данном случае существует только одно правило с истинной условной частью, то механизм вывода сразу же выполняет его заключительную часть и образец «дорога ухабистая» заносится в рабочую память. При попытке вторично применить эти правила получается, что можно применить лишь правило 1 , поскольку правило 2 уже было применено и выбыло из числа кандидатов. К этому времени содержимое рабочей памяти было дополнено новым образцом – результатом применения правила 2, поэтому условная часть правила 1 становится истинной, и содержимое рабочей памяти пополняется образцом его заключительной части - «использовать джип». В итоге правил, которые можно было бы применять, не остается, и система останавливается.

Обратный вывод – это способ, при котором на основании фактов, требующих подтверждения, чтобы выступать в роли заключения, исследуется возможность применения правила, пригодного для подтверждения. Допустим, что цель – это «использовать джип», и исследуем сначала возможность применения правила 1, подтверждающего этот факт. Поскольку образец «намерение – отдых» из условной части правила 1 уже занесен в рабочую память, то для достижения цели достаточно подтвердить факт «дорога ухабистая». Однако если принять образец «дорога ухабистая» за новую цель, то потребуется правило, подтверждающее этот факт. Поэтому исследуем возможность применения правила 2. Условная часть этого правила в данный момент является истинной, поэтому правило 2 можно сразу же поменять, рабочая память при этом пополнится образцом «дорога ухабистая», и в результате возможности применения правила 1 подтверждается цель «использовать джип».

В случае обратного вывода условия останова системы очевидны: либо достигается первоначальная цель, либо кончаются правила, применимые для достижения цели в ходе вывода. Что касается прямого вывода, то, как было указано выше, отсутствие применимых правил также является условием останова. Однако система останавливается и при выполнении некоторого условия, которому удовлетворяет содержимое рабочей памяти, например, путем проверки появления образца «использовать джип». Доказано, что для обратных выводов характерна тенденция исключения из рассмотрения правил, не имеющих прямого отношения к заданной цели, что позволяет повысить эффективность вывода.

Продукционные системы просты в применении и благодаря хорошей подготовленности средств разработки позволили создать большое число систем, основанных на использовании знаний. Продукционные системы в отличие от фреймовых и других систем не имеют такие функции, как, например, установление высокоуровневых отношений между фреймами, но, с другой стороны, благодаря этому упрощается проектирование системы и ее создание. В будущем, вероятно, найдут применение не только чисто продукционные системы, но и комбинации их, например, с фреймовыми системами. Вернуться