Исчисления высказываний.
Эквивалентные преобразования формул нужны для того, чтобы привести структуру целевой теоремы к канонической форме (КФ). КФ представляет собой приведенную нормальную форму с дизъюнктами вместо дизъюнктивных формул и с некоторыми другими принципиальными особенностями, которые будут рассмотрены позже.
Если в посылках и целевой теоремы присутствуют формулы, не соответствующие указанным требованиям, то они должны быть корректно заменены эквивалентными формулами. Это позволяет определить правила эквивалентных преобразований (табл. 3.4), где используются два новых метасимвола.
* ( конверт) - для обозначения общезначимых формул
= (равенство) - для обозначения равенства формул.
Таблица 3.4
| № правила | Правила эквивалентных преобразований формул Исчисления высказываний |
F 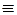 G=( F® G) Ù (G® F ) G=( F® G) Ù (G® F )
| |
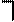 2 2
| F®G = F 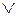 G G
|
| а. FÚG=GÚF; б. FÙG=GÙF | |
| a. (FÚG) ÚH=FÚ(GÚH); б. (FÙG)ÙH=FÙ(GÙH) | |
| а. FÚ(GÙH)=(FÚG)Ù(FÚH); б. FÙ(GÚH)=(FÙG)Ú(FÙH) | |
 6 6
| a. FÚ = F; б. FÙ * =F |
  7 7
| a.FÚ * = *; б. FÙ = |
     8 8
| a.FÚ F=*; б. FÙ F= |
| ( F)=F | |
a.ù (F ÚG)=ù F Ùù G; б.ù (FÙG)=ù FÚù G   
|
Других правил эквивалентных преобразований нет.
Пример: Получим дизъюнктивную форму для формулы
(P Úù Q) ®R
(PÚù Q) ®R=ù ( P Úù Q)Ú R= ( по п. 2)
=( ù P Úù (ù Q))Ú R= ( по п. 10а)
=( ù P ÙQ ) Ú R ( по 9 ). Вернуться
Дата добавления: 2016-03-27; просмотров: 705;
