Дедуктивного рассуждения).
Стереотипы выработаны за многие десятки лет, а некоторые за многие сотни лет и позволяют осуществлять корректные, т.е. без нарушения отношения логического следования, переходы от одних теорем к другим с целью приведения структуры рассуждения к канонической форме (к приведенной КНФ). Сущность канонической формы будет раскрыта в 3.2.2.6, а сейчас, до обсуждения правил вывода, введем ряд новых понятий, без которых это обсуждение невозможно.
Понятие «отношение логического следования».
Формула G является логическим следствием формул F1,F2,...,Fn тогда и только тогда, когда для каждой интерпретации I, в которой (F1 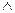 F2
F2 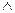 ,...
,... 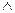 Fn.)- истина, G также истина. F1,F2,...,Fn называются посылками, а G - заключением в отношении логического следования.
Fn.)- истина, G также истина. F1,F2,...,Fn называются посылками, а G - заключением в отношении логического следования.
Понятие «необходимые и достаточные условия логического следования».
 Формула G тогда и только тогда является логическим следствиемF1,F2,...,Fn, когда формула ((F1
Формула G тогда и только тогда является логическим следствиемF1,F2,...,Fn, когда формула ((F1 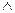 F2
F2 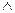 ,...
,... 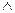 Fn.)
Fn.) 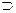 G) - общезначима или, когда формула (F1
G) - общезначима или, когда формула (F1 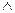 F2
F2 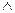 ,...
,... 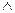 Fn Ù G) -противоречива.
Fn Ù G) -противоречива.
Понятие «теорема в дедуктивном рассуждении.
Если формула G является логическим следствием формул F1,F2,...,Fn, то формула ((F1 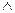 F2
F2 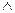 ,...
,... 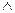 Fn )
Fn ) 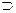 G) называется теоремой, а G называется заключением теоремы.
G) называется теоремой, а G называется заключением теоремы.
Понятие «доказательство в дедуктивном рассуждении» (т.е. в исчислении).
Доказательство - это аргументированное обоснование того, каким образом заключение в теореме логически следует из её посылок. Представляется доказательство в виде упорядоченной последовательности (следа) умозаключений, в результате которых устанавливается истинностное значение заключения.
Теперь о правилах вывода в исчислениях высказываний.
 Для обозначения отношения логического следования введем новый метасимвол (горизонтальная черта). Будем использовать этот метасимвол для разделения теорем – посылок и теорем – заключений. Над чертой будем записывать список теорем-посылок, под чертой - теорему-заключение. Указанная форма записи теорем будет свидетельствовать о том, что теорема – заключение является логическим следствием теорем – посылок.
Для обозначения отношения логического следования введем новый метасимвол (горизонтальная черта). Будем использовать этот метасимвол для разделения теорем – посылок и теорем – заключений. Над чертой будем записывать список теорем-посылок, под чертой - теорему-заключение. Указанная форма записи теорем будет свидетельствовать о том, что теорема – заключение является логическим следствием теорем – посылок.
Метасимвол ; (точку с запятой) будем использовать в качестве разделителя в списке теорем.
Метасимвол , (запятую) будем использовать в качестве разделителя посылок внутри теоремы, имитирующего конъюнктивную связку.
 Метасимвол (прямоугольник) будем использовать для обозначения противоречивых формул.
Метасимвол (прямоугольник) будем использовать для обозначения противоречивых формул.
Рассмотрим следующий пример использования отношения логического следования:
Если барометр падает, то будет дурная погода;
Барометр падает
 Будет дурная погода
Будет дурная погода
 Перечень правил вывода следующий:
Перечень правил вывода следующий:
 1)
1)  Г É F ; Г É Y 2) Г É FÙY 3) Г É FÙY 4) Г É F
Г É F ; Г É Y 2) Г É FÙY 3) Г É FÙY 4) Г É F

 Г É FÙY Г É F Г ÉY Г ÉYÚY
Г É FÙY Г É F Г ÉY Г ÉYÚY
5) 
 Г É Y 6) Г,F É Y; Г,C É Y; Г É FÚC 7) Г,F É Y
Г É Y 6) Г,F É Y; Г,C É Y; Г É FÚC 7) Г,F É Y
Г É FÚY Г ÉY Г É YÉY



 8) Г É F ;Г É F ÉY 9) Г, ù F É 10) Г É F;Г É ù F
8) Г É F ;Г É F ÉY 9) Г, ù F É 10) Г É F;Г É ù F
 Г ÉY Г É F Г É
Г ÉY Г É F Г É
11) Г,F,Y, Г1 É C 12) Г É F

 Г, Y,F, Г1 É C Г, Y É F
Г, Y,F, Г1 É C Г, Y É F
Правила 1, 2 и 3, эксплуатируя сущность конъюнктивной связки, позволяют упростить модель теоремы.
Правила 4 и 5, эксплуатируя сущность дизъюнктивной связки, позволяют в заключении теоремы вводить новые дополнительные формулы.
Правило 6 формирует способ рассуждения «разбор» двух возможных случаев. Если при выполнении посылок Г справедливо Ф или Х, а Y справедливо при выполнении условий Г и Ф , а также при выполнении условий Г и Х, то Y всегда справедливо при выполнении посылок Г, что устанавливается путем рассмотрения двух возможных случаев:
а) выполнены условия Г и Ф;
б) выполнены условия Г и Х.
Правило 7 формализует прием эквивалентной перефор-мулировки теоремы, позволяющей одну из посылок теоремы помещать в заключение в виде посылки.
Правило 8 - правило вывода (отделения), modus ponens, введенное ещё Аристотелем. Оно указывает, как можно освобождаться от посылки в заключении.
Правило 9 - формализует «рассуждение от противного». Пусть, условие Г и ù Ф могут одновременно выполняться. Приходя к противоречию, заключаем, что из выполнимости Г всегда вытекает выполнимость Ф.
Правило 10 - это правило «обнаружения противоречия».
Правило 11 - перестановка посылок не влияет на истинность заключения.
Правило 12 - добавляя лишнюю посылку, мы не нарушаем истинность заключения теоремы.
Выводы: правила вывода 1-12 являются функционально полным набором правил, применяя которые к исходным аксиомам и доказанным теоремам, можно в конце концов получить доказательство истинного значения заключения в теореме - цели. Однако обязательными требованиями построения доказательства с помощью правил вывода 1-12 являются следующие:
1) исходными посылками должны быть только аксиомы и доказанные теоремы.
2) с помощью правил вывода 1-12 (и только этих правил) можно строить композиции аксиом и доказанных теорем, стремясь в итоге получить заключение теоремы-цели. Эти два требования соответствуют стереотипу классического дедуктивного рассуждения, иногда называемого прямой дедукцией, т.е. рассуждения от истинных абстрактных посылок (аксиом и доказанных теорем) к истинному конкретному заключению. Примеры несоблюдения требований:
а) Все металлы - элементы;
б) Бронза - металл
 Бронза - элемент
Бронза - элемент
Вывод ошибочен: бронза не является элементом. Здесь нарушен закон тождества, который запрещает в процессе данного умозаключения в одно и то же понятие вкладывать различное содержание. В посылках употреблен металл не водинаковом смысле. В а) металл - химический элемент, а в б) - металл - это вещество, используемое в хозяйстве, производстве.
‚ Бэкон и Гоббс были египтянами
 Бэкон и Гоббс были идеалистами
Бэкон и Гоббс были идеалистами
Некоторые идеалисты были египтянами
Вывод в умозаключении верный, однако, обе посылки ложны: Бэкон и Гоббс были англичанами и материалистами.
Практика показала, что способ доказательства теорем прямой дедукцией чрезвычайно неэффективен по следующей причине. Структура композиций на промежуточных шагах преобразований является случайной в связи с тем, что не существует критериев и управляющих воздействий, которые целенаправленно ориентировали бы эти композиции к заданной цели. Поэтому не исключена возможность ухода в сторону от цели, что чаще всего и бывает на практике. Из этого вытекает глобальный вывод о неэффективности прямой дедукции при доказательстве теорем. В связи с этим правила 1-12 чаще всего используются для приведения структуры теоремы к канонической форме. Вернуться
Дата добавления: 2016-03-27; просмотров: 959;
