Свойство взаимности

Пользуясь методом контурных токов можно установить еще одно важное свойство линейных электрических цепей – свойство взаимности (принцип взаимности).

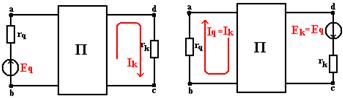
Пусть в схеме произвольной конфигурации единственный источник ЭДС E_q действует в ветви с сопротивлением r_q в направлении от точки b к точке а (рис. 1.6,а) и создает в ветви с сопротивлением r_k ток I_k, направленный от точки d к точке с.

Тогда такой же единственный источник ЭДС E_k = E_q, включенный в ветвь с сопротивлением r_k и действующий в направлении от d к c (рис. 1.6,б), создаст в ветви с сопротивлением r_q ток I_q, направленный от b к а и равный току I_k.

На рис. 1.6,а изображены ветви ab и cd с сопротивлениями r_q и r_k, а остальная часть схемы, не содержащая источники энергии, условно показана в виде прямоугольника с буквой П (пассивная).

Для доказательства свойства взаимности воспользуемся выражением, определяющем ток в любом контуре. Пусть ветвь cd является частью контура k, а ветвь ab входит в состав другого контура q и, как указано, других источников ЭДС, кроме Е_q, эта цепь не содержит. Контуры выберем так, чтобы ветви ab и cd вошли каждая в свой контур, соответственно q и k.

а) б)

Рисунок 1.6

Тогда ток I_k в контуре k, равный току ветви dc, определится выражением

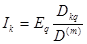. (1.26)

Если источник ЭДС Е_q переставить в ветвь cd контура k (рис. 1.6,б), то после этого ток I_q в контуре q, т.е. ток ветви ab, определится выражением

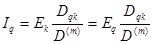. (1.27)

Алгебраическое дополнение вида D_kq получается из определителя D^(m) путем вычеркивания в нем столбца k и строки q и умножения получаемого определителя на (-1)^k+q, а алгебраическое дополнение вида D_qk – вычеркиванием столбца q и строки k и умножением получаемого определителя на (-1)^q+k. Так как в контурных уравнениях общие сопротивления r_qk и r_kq равны друг другу, то и D_kq = D_qk. Следовательно, при равенстве ЭДС E_q = E_k токи в ветвях cd и аb равны друг другу.