Общие соотношения между контурными токами, сопротивлениями и ЭДС цепи произвольной конфигурации

Для схемы, имеющей k независимых контуров, уравнения, аналогичные (1.4), запишутся в виде

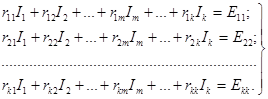(1.12)

В этих уравнениях сопротивление с двумя одинаковыми индексами (вида r_mm) называется собственным сопротивлением контура m , а сопротивление вида r_mk = r_km (c двумя различными индексами) называется общим сопротивлением контуров k и m. Правые части уравнений называются контурными ЭДС. Каждая из контурных ЭДС вида Е_mm равна алгебраической сумме ЭДС всех источников в ветвях контура m. Положительные знаки в каждом уравнении (1.12) должны быть взяты для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.

Решая систему уравнений (1.12) при помощи определителей относительно любого из токов, например I_m, получаем:

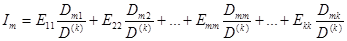, (1.13)

где

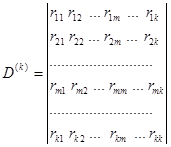- определитель системы уравнений; (1.14)

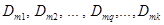- алгебраические дополнения определителя 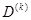, причем 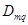получается из 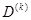путем вычеркивания m-ного столбца и q-той строки и умножения полученного определителя на (-1)^m+q. При этом сопротивления вида r_mm и r_km нужно записывать в выражении (1.14) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1.12).

Для решения общей задачи расчета неизвестных токов во всех ветвях линейной электрической цепи можно выбрать один из двух основных методов расчета: узловых потенциалов или контурных токов.

Метод узловых потенциалов целесообразно использовать, когда число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров (у – 1 < k), а метод контурных токов при у -1 > k.