Эквивалентная проводимость g не зависит от ЭДС, в то время как эквивалентная ЭДС Е зависит не только от ЭДС ветвей, но и от их проводимостей.

Несмотря на неизменность токов и напряжений в той части схемы, которая не затронута преобразованием, мощность, развиваемая источниками ЭДС до преобразования, не равна мощности, развиваемой эквивалентным источником ЭДС после преобразования схемы.

Если к узлам 1 и 2 (рис. 1.4,а) присоединены кроме m ветвей с источниками ЭДС еще n ветвей с источниками тока, то при вычислении эквивалентной ЭДС нужно учесть токи заданных источников тока:

. (1.21)

Принцип наложения

При рассмотрении метода контурных токов было получено выражение для определения контурных токов

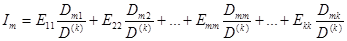. (1.22)

Если в уравнении (1.22) заменить все контурные ЭДС алгебраическими суммами ЭДС ветвей, то после группировки слагаемых получится выражение для контурного тока I_m в виде алгебраической суммы составляющих токов, вызванных каждой их ЭДС ветвей в отдельности. При этом каждая составляющая тока равна произведению ЭДС ветви на алгебраическую сумму коэффициентов вида , входящих в уравнение (1.22).

Это важное свойство носит название принципа наложения и непосредственно вытекает из линейности уравнений электрического состояния для цепей с линейными элементами. Принцип наложения справедлив не только для контурных токов, но и для токов ветвей, так как систему независимых контуров всегда можно выбрать так, что рассматриваемая ветвь войдет только в один контур, т.е. контурный ток будет равен действительному току ветви.

Рассмотрим электрическую схему, приведенную на рис. 1.5.

Рисунок 1.5

Пользуясь методом контурных токов, запишем следующие уравнения:

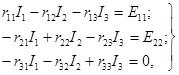(1.23)

где

;

Из уравнений (1.23):

, (1.24)

где

; ; ;

; .

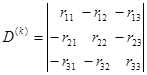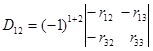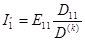Аналогично определяются токи I₂ и I₃.

Если в выражении (1.24) контурные ЭДС заменить через ЭДС ветвей, то получим:

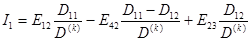. (1.25)

Из выражения (1.25) следует, что контурный ток I₁ равен алгебраической сумме составляющих токов, вызываемых каждой из ЭДС в отдельности. Кроме того, этот контурный ток равен действительному току ветви с сопротивлением r₁ и ЭДС Е₁₂, так как по этой ветви другие контурные токи не замыкаются.

Таким образом, при определении токов ветвей при помощи принципа наложения можно поочередно оставлять в схеме по одной ЭДС, считая все остальные ЭДС источников равными нулю, но сохраняя в схеме их внутренние сопротивления. Действительные токи ветвей определятся как алгебраические суммы токов, вызываемых каждой ЭДС. Если схема содержит не только источники ЭДС, но и источники тока, то следует найти составляющие токов, вызываемые каждой ЭДС и каждым источником тока, посте чего определить действительные токи путем алгебраического суммирования этих составляющих.