Теорема об активном двухполюснике

Выделим в электрической цепи одну ветвь 2-2́ с сопротивлением r, присоединенную в точках 1-1́ к активному двухполюснику (рис. 1.9).

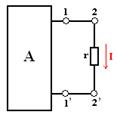
Рисунок 1.9

Покажем, что для расчета тока I в ветви 2-2́ активный двухполюсник можно заменить источником ЭДС и пассивным двухполюсником. Чтобы найти ЭДС источника, разомкнем цепь между точками 1 и 2 (рис. 1.10,а) и определим разность потенциалов U_х опытным или расчетным путем.

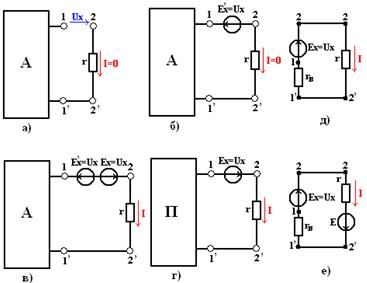
Рисунок 1.10

Затем подключим к точкам 1 и 2 источник с ЭДС 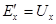, направленной навстречу U_x (рис. 1.10,б). Ток в ветви 2-2́ останется равным нулю, т.к. при этом разность потенциалов любых двух точек не изменилась. Схема на рис. 1.4,б отличается от заданной на рис. 1.3 тем, что в ней между точками 1 и 2 включен источник ЭДС 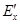и ток в ветви 2-2́ равен нулю. Эта схема будет эквивалентна заданной, если между точками 1 и 2 ввести еще одну ЭДС 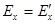, противоположно направленную 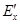(рис. 1.10,в).

По принципу наложения ток I в ветви 2-2́ эквивалентной схемы (рис. 1.10,в) а значит и заданной (рис. 1.9), найдем как алгебраическую сумму токов, создаваемых каждым источником. Но все источники, находящиеся внутри активного двухполюсника, совместно с источником ЭДС 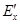не вызывают ток в ветви 2-2́ (рис. 1.10,б). Поэтому ток в ветви 2-2́, создаваемый одним источником ЭДС Е_х (рис. 1.10,г), равен действительному току в этой ветви (рис. 1.9):

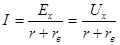, (1)

где r_в – входное сопротивление пассивного двухполюсника, получающегося из заданного активного после того, как все ЭДС источников напряжения и все токи источников тока приняты равными нулю.

В частности, при r = 0, т.е. при коротком замыкании ветви 2-2́, 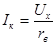, т.е. входное сопротивление активного двухполюсника можно определить как отношение напряжения холостого хода к току короткого замыкания:

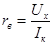. (2)

Тогда

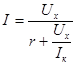. (3)

В общем случае сопротивление r может быть входным сопротивлением пассивного двухполюсника, присоединенного к зажимам 1-1́ заданного активного двухполюсника.

Уравнение (1) представляет собой математическое выражение теоремы об активном двухполюснике, называемой также теоремой об эквивалентном генераторе или теоремой Гельмгольца и Тевенена. Эта теорема формулируется следующим образом: если активная цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Уравнению (1) соответствует эквивалентная схема, показанная на рис. 1.10,д, где активный двухполюсник представлен в простейшей форме, в виде неразветвленной цепи с источником ЭДС Е_х = U_х и сопротивлением r_в. Таким образом, активный двухполюсник по отношению к присоединенной ветви с сопротивлением r можно рассматривать как источник с внутренним сопротивлением r_в и ЭДС Е_х, равной напряжению U_х между зажимами двухполюсника при разомкнутой ветви 2-2́ .

Если рассматриваемая ветвь содержит не только сопротивление r, но и источник ЭДС Е, то ток в этой ветви

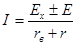, (4)

где ЭДС Е берется с положительным знаком, когда обе ЭДС Е_х и Е действуют в одном и том же направлении (рис. 1.10,е), и с отрицательным, когда ЭДС Е направлена навстречу Е_х.

В эквивалентной схеме активного двухполюсника (рис. 1.10,д), так же как при любых других преобразованиях схем с источниками энергии, мощность источника с эквивалентной ЭДС и потери в сопротивлении r_в в общем случае не равны соответственно суммарной мощности источников энергии в реальной цепи и потерям в сопротивлениях ветвей активного двухполюсника.