Теорема о компенсации

В электрической схеме, показанной на рис. 1.7,а, выделена ветвь с сопротивлением r₁ и током I₁.

а) б) в)

Рисунок 1.7

Включим в эту ветвь два источника ЭДС Е1^́ и Е1 (рис. 1.7,б), численно равными напряжению U₁ = r₁I₁ и направленными навстречу друг другу. Очевидно, что при этом токи во всех ветвях схемы не изменятся. При переходе из точки d в точку с потенциал повышается на величину ЭДС Е1^́ = U₁, а при переходе из точки с в точку b понижается на ту же величину, вследствие чего потенциалы точек d и b равны. Эти точки можно закоротить, как показано на рисунке 1,б синей линией, т.е. источник ЭДС Е1^́ = U₁ и сопротивление r₁ удалить из схемы, не изменив токи во всех ветвях (рис. 1.7,в).

Из сравнения схем на рис. 1.7,а и 1.7,в следует, что любое сопротивление можно заменить источником ЭДС, направленной навстречу току и равной напряжению на этом сопротивлении. Это положение называется теоремой о компенсации.

Двухполюсники

При исследовании процессов в сложных электрических цепях часто необходимо определить ток, напряжение и мощность только в одной ветви. В этом случае выделяется ветвь, присоединенная к сложной цепи в двух точках. Часть электрической цепи произвольной конфигурации с двумя выделенными зажимами, именуемыми полюсами, называется двухполюсником.

Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источники электрической энергии,- пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной – сопротивлением r_в. Поэтому на эквивалентной схеме пассивный двухполюсник может быть представлен одним элементов – сопротивлением r_в, называемым внутренним или входным сопротивлением пассивного двухполюсника.

Если известна схема пассивного двухполюсника, то для определения входного сопротивления r_в нужно тем или иным способом ее «свернуть» относительно двух заданных режимов.

Рассмотрим схему на рис. 1.8,а.

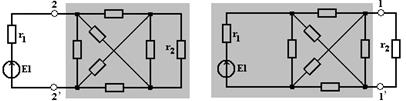
а) б)

Рисунок 1.8

Если выделить в этой схеме ветвь с источником Е1 и сопротивлением r₁, то остальную часть схемы можно рассматривать относительно зажимов 2-2́ как пассивный двухполюсник. Часть той же схемы относительно зажимов 1-1́ ветви с сопротивлением r₂ можно рассматривать как активных двухполюсник.