Общее свойство минимально-фазовых устойчивых звеньев
Общим показателем свойств звена является принадлежность нулей передаточной функции к левой полуплоскости. Представляя передаточную функцию в форме (1.6), комплексный коэффициент передачи можно выразить как
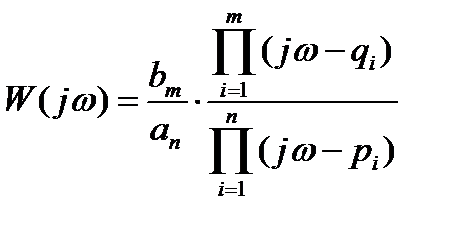 . (1.27)
. (1.27)
Рассмотрим сомножитель числителя jω-qi. Эта разность представляет собой вектор, начало которого лежит в точке qi, а конец на мнимой оси в точке jω. Фаза этого вектора характеризует поворот его относительно вещественной оси против часовой стрелки.
На рисунке 1.10 построены два таких вектора для различных положений точки qi, обозначенных qi' и qi''. Из построения видно, что при одном и том же значении модуля комплекса jω-qi его фаза φ меньше в том случае, когда qi лежит в левой полуплоскости. Поэтому звенья, все нули передаточной функции лежат в левой полуплоскости (Re qi<0), называются минимально-фазовыми. Звенья, передаточные функции которых имеют хотя бы один нуль, лежащий в правой полуплоскости (Re qi.>0), называются неминимально-фазовыми.
Рисунок 1.10 – Минимально- и неминимально-фазовые звенья
Для минимально-фазовых устойчивых звеньев между амплитудно-частотной и фазочастотной характеристиками существует однозначная зависимость и, следовательно, амплитудно-частотная характеристика однозначно определяет передаточную функцию системы.
Итак, если известна амплитудно-частотная характеристика звена и известно, что звено устойчивое и минимально-фазовое, то этого достаточно для того, чтобы найти все его частотные характеристики и, следовательно, полностью охарактеризовать поведение системы при любых сигналах, поступающих на вход.
Для минимально-фазовой системы определение приближённого значения фазы φi(ωi) можно проводить непосредственно по среднему наклону ЛАЧХ в частоте ωi без построения ЛФЧХ. При этом
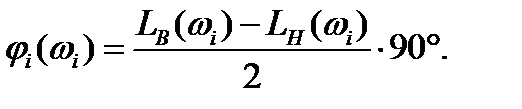 (1.28)
(1.28)
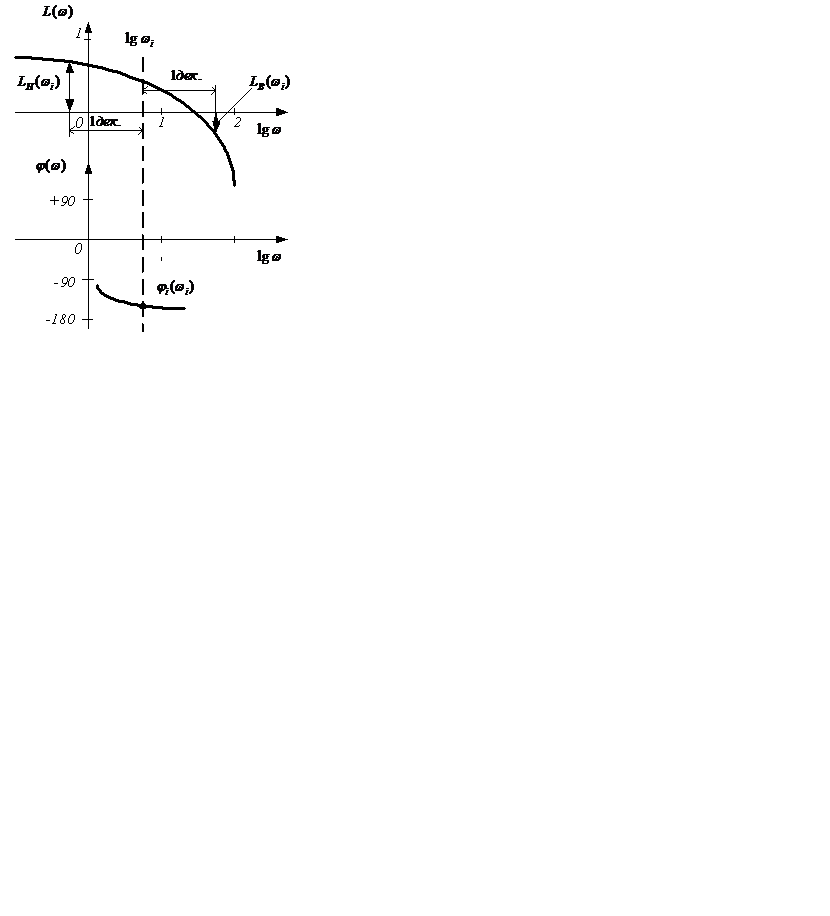
Рисунок 1.11 – Определение фазы системы по амплитуде
При этом LВ(ωi) и LН(ωi) значения ЛАЧХ при частотах, отстоящих от ωi на одну декаду в сторону увеличения и уменьшения частот соответственно.
Дата добавления: 2016-04-11; просмотров: 758;
