Логарифмические частотные характеристики
В практических расчетах наряду с использованием АФЧХ широко используются так называемые логарифмические амплитудные фазовые частотные характеристики ЛАФЧХ или просто логарифмические частотные характеристики. При этом различают логарифмические амплитудные частотные характеристики ЛАЧХ и логарифмические фазовые частотные характеристики ЛФЧХ.
ЛАЧХ называют зависимость L(ω)=lgА(ω) от lg (w),
ЛФЧХ называют зависимость j(ω)от lg (w).
| 1 дек. |
w 
|
| х = lg(w) |
Рисунок 1.6 – Ось абсцисс
Интервал частот, кратный 10, называется декадой. Одна дек на чертежах равна 50 мм.
По оси ординат при построении ЛАЧХ откладывается величина L(w) в логарифмическом масштабе. Один лог на чертежах равен 50 мм.
Логарифм может быть разбит на более мелкие единицы
1 лог = 10 дл (децилог) = 20 дб (децибел), таким образом:
Y [дл] = 10 lg k,
Y [дб] = 20 lg k.
По оси ординат при построении ЛФЧХ откладывается величина j(w) в градусах, т.е. полулогарифмический масштаб. На чертежах отрезок 90° равен 45 мм.

| L(w) |
| y = lg A(w) |
| 100 |
| 10 |
| 1 |
| 0,1 |
| 0,01 |
| лог. |
| 1 |
| -1 |
| 0 |
| 2 |
| -2 |
| дл. |
| 0 |
| 10 |
| -10 |
| 20 |
| -20 |
| дб. |
| 0 |
| 20 |
| -20 |
| 40 |
| -40 |
Рисунок 1.7 – Ось ординат
Достоинства ЛФЧХ:
1. При использовании ЛЧХ представляется возможным изображать величины, несоизмеримые в равномерном масштабе (например, от 0,01 до 1000).
2. При использовании ЛЧХ операция умножения коэффициентов усилительных звеньев заменяется операцией сложения ординат характеристик этих звеньев.
При использовании логарифмического масштаба нелинейные зависимости превращаются в прямые линии.
Устойчивость звена
Из рассмотрения выражения (1.8) следует, что устойчивость системы зависит от того, в какой области лежат корни pi.. Для линейных систем определение устойчивости объекта или звена может быть сформулировано более жёстко, чем для общего случая. Линейное звено является устойчивым, если после окончания внешнего воздействия его состояние с течением времени возвратится к исходному.
Единичный импульс может быть рассмотрен как кратковременное воздействие. В таком случае об устойчивости линейного звена можно судить по значению хВЫХ(t) при t→∞: звено устойчиво, если
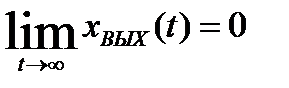 ; (1.21)
; (1.21)
звено неустойчиво, если
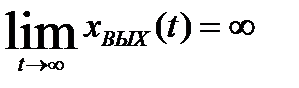 ; (1.22)
; (1.22)
звено нейтрально, если
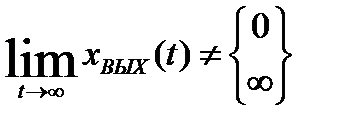 . (1.23)
. (1.23)
Если хВЫХ(t) при t→∞ является периодической функцией времени, т.е.
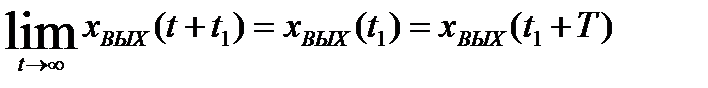 , (1.24)
, (1.24)
где Т – период колебаний, то звено называется консервативным.
Каждому вещественному значению рi в выражении (1.8) соответствует слагаемое вида
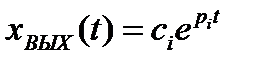 , (1.25)
, (1.25)
где
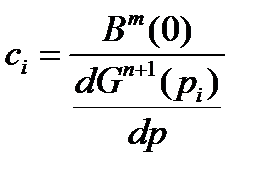 .
.
Комплексной паре корней характеристического уравнения
pi=αi+jωi; pi=αi-jωi
соответствует слагаемое вида
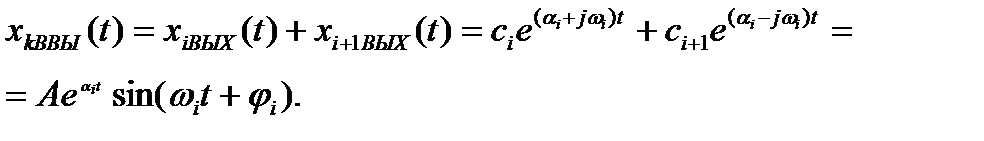 (1.26)
(1.26)
Следует различать три случая расположения корней, когда вещественная часть корня: 1) отрицательна (αi<0); 2) положительна (αi>0); 3) равна нулю (αi=0).
В первом случае корень лежит в левой полуплоскости корней, т.е. левее мнимой оси (см. р1, р2, р3 на рисунке 1.8), во втором случае – в правой полуплоскости, т.е. правее мнимой оси (см. р4, р5 ,р6 на рисунке 1.8); в третьем случае – на мнимой оси (см. р7, р8, р9 на рисунке 1.8).
Рисунок 1.8 – Расположение корней характеристического уравнения
В зависимости от расположения корней относительно мнимой оси характер изменения составляющих хiВЫХ(t) во времени различен. Если αi>0, то соответствующая составляющая при t→∞ стремится к бесконечности и, следовательно, хВЫХ(t)→∞, т.е. звено неустойчиво.
Если αi<0, то соответствующая составляющая при t→∞ стремится к нулю; следовательно, если все составляющие, число которых конечно, удовлетворяют этому условию, то хВЫХ(t)→0, т.е. звено асимптотически устойчиво.
Если αi=0 при t→∞, то составляющая остаётся конечной и не равна нулю, т.е. звено нейтрально ил консервативно. Оно относится также к устойчивым, но неасимптотическим звеньям.
На рисунке 1.9 для каждого случая расположения корней показаны графики при вещественном корне (а, б, в) и при паре сопряжённых комплексных корней (г, д, е).
а) б) в)
г) д) е)
Рисунок 1.9 – Графики xiВЫХ при различных корнях рi
Таким образом, необходимым и достаточным условием асимптотической устойчивости линейного звена является отрицательное значение вещественной части всех полюсов функции W(p), т.е. все полюсы должны лежать в левой полуплоскости р.
Дата добавления: 2016-04-11; просмотров: 715;
