Дифференцирующее звено

На практике не существует реального элементе, в котором на выходе точно воспроизводилась бы производная от любого входного сигнала. Однако, составляя структурную схему системы, её можно так разделить на звенья, что введение понятия дифференцирующего звена будет вполне обосновано. В этом случае выходная величина х_ВЫХ(t) зависит от входной величины х_ВХ(t) как производная (идеальное дифференцирующее звено)

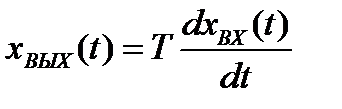, (2.12)

Переходя к изображениям, получим

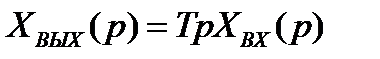, (2.13)

Передаточная функция звена

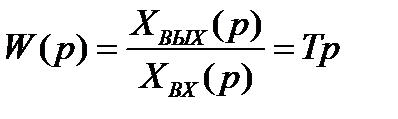, (2.14)

На структурных схемах изображается (рисунок 2.7)

Рисунок 2.7 – Дифференцирующее звено

Изображение выходной величины равняется

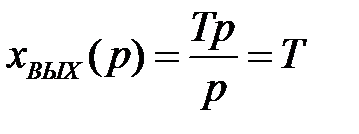, (2.15)

тогда переходная функция равна

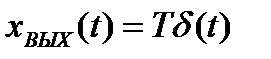(2.16)

и представлена на рисунке 2.8, а.

Перейдём к частотным характеристикам, заменим р на jω. Комплексный коэффициент передачи

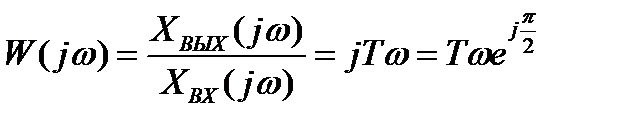. (2.17)

Частотный годограф и частотные характеристики показаны на рисунке 2.8, б, в и г. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) имеет положительный наклон +1 лог/дек (рисунок 2.8,г). Логарифмическая фазо-частотная характеристика (ЛФЧХ) проходит параллельно оси абсцисс и отстоит от неё на +90° (рисунок 2.8, г).

а) б) в)

г)

Рисунок 2.8 – Переходная функция (а), годограф (б),

частотные характеристики (в), ЛАЧХ и ЛФЧХ (г) дифференцирующего звена