Усилительное (пропорциональное) звено

Самым простым является звено, выходная величина которого прямо пропорциональна входной величине.

Уравнение такого звена во временной области

x_ВЫХ(t) =k x_ВХ(t),

(2.1)

где k – коэффициент передачи (усиления) звена.

Примерами такого звена являются: делитель напряжения, усилитель постоянного тока, рычажная передача, редукторная передача и др.

Предполагается, что передача сигнала от входа к выходу производится мгновенно без какой-либо инерции. Поэтому пропорциональные звенья называются безынерционными.

Если перейти к операторной форме записи, то на выходе

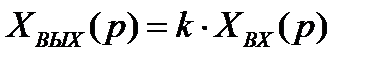, (2.2)

Передаточная функция звена

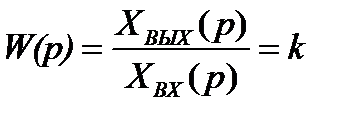, (2.3)

На структурных схемах изображается так, как показано на рисунке 2.1.

Рисунок 2.1 – Изображение усилительного звена

Переходя от коэффициента усиления к переходной функции, получаем

h(t)=x_ВЫХ(t)=k 1(t). (2.4)

Графическое изображение переходной функции усилительного звена показано на рисунке 2.2. Эта функция соответствует идеальному пропорциональному звену.

Рисунок 2.2 – Переходная функция усилительного звена

Комплексный коэффициент передачи

. (2.5)

Годограф комплексного коэффициента передачи W(jω) при 0<ω<∞ имеет вид точки, сдвинутой на расстоянии k от нуля по вещественной оси (рисунок 2.3,а), а зависимости P(ω) и Q(ω) показаны на рисунке 2.3, б.

а) б)

Рисунок 2.3 – Зависимости W(jω), P(ω) и Q(ω)

ЛАЧХ безынерционного звена представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на расстоянии lgk. ЛФЧХ совпадает с осью абсцисс (рисунок 2.4).

Рисунок 2.4 – ЛАЧХ и ЛФЧХ усилительного звена

1.2 Интегрирующее звено

Идеальным интегрирующим звеном называется звено, выходная величина которого пропорциональна интегралу входной величины

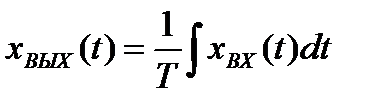, (2.6)

где Т – постоянная времени.

Такие звенья называются интегрирующими. Примерами реальных элементов, эквивалентные схемы которых сводятся к интегрирующему звену являются6 электрический конденсатор, вращающийся вал, гидравлический резервуар, гидравлический усилитель и др.

Переходя к изображениям, получим

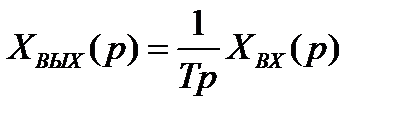(2.7)

Передаточная функция звена

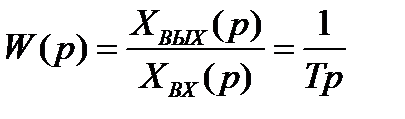, (2.8)

На структурных схемах изображается (рисунок 2.5)   Рисунок 2.5 – Интегрирующее звено

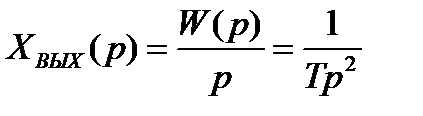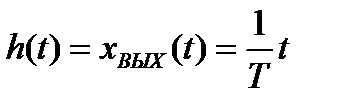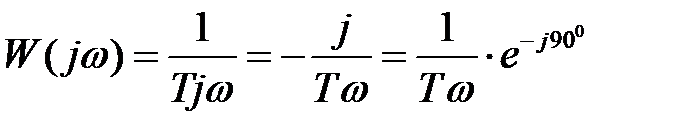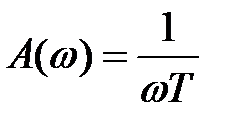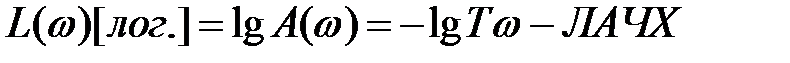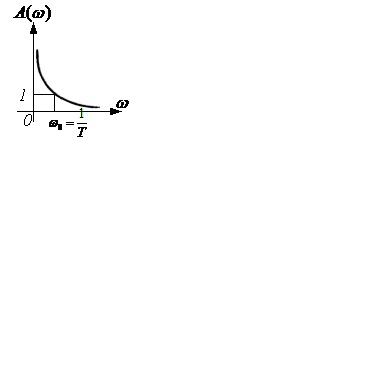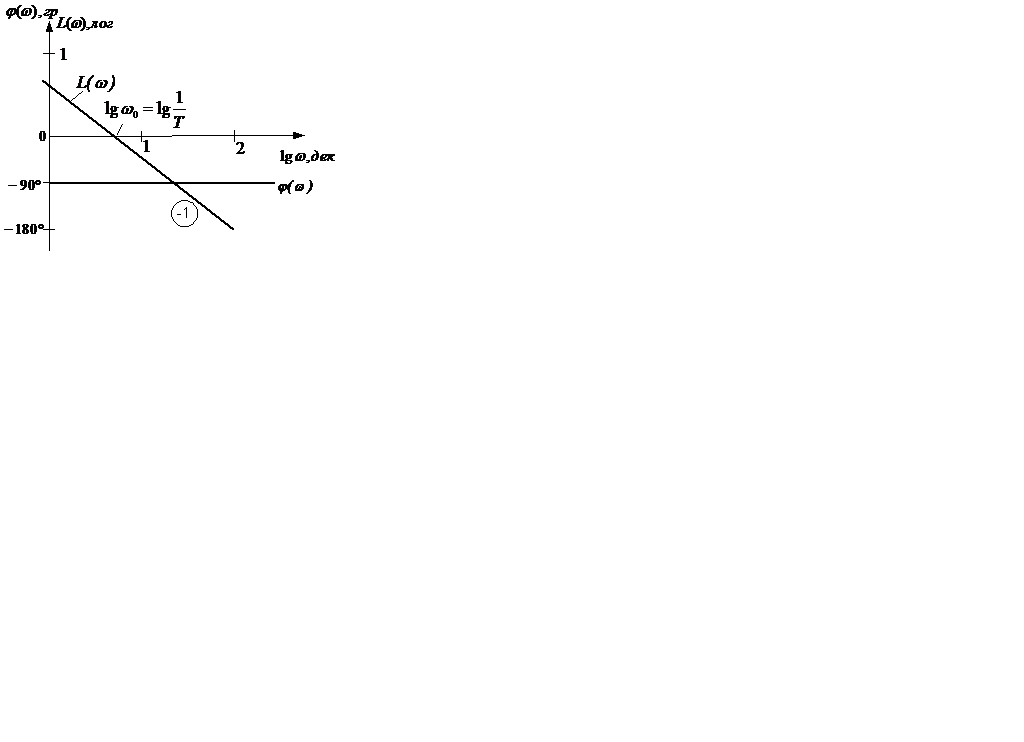
Изображение выходной величины равняется , (2.9) тогда переходная функция интегрирующего звена (2.10) рисунок 2.6, а. Перейдём к частотным характеристикам, заменим р на jω ; ; , . (2.11) Частотный годограф и частотные характеристики интегрирующего звена показаны на рисунке 2.6,б и в,г. а) б) в) г) д)     Рисунок 2.6 – Переходная функция (а), годограф (б), частотные характеристики (в), ЛАЧХ и ЛФЧХ (г) интегрирующего звена   Логарифмическая амплитудно-частотная характеристика L(ω)=lg|W(jω)| в функции lgω имеет вид прямой с наклоном -1 лог/дек. График логарифмической амплитудно-частотной характеристики L(ω) (рисунок 2.6,г) для интегрирующего звена пересекает ось абсцисс при 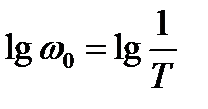. Логарифмическая фазо-частотная характеристика φ(ω) (рисунок 2.6,г) представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на -90°.