Коэффициент корреляции рангов Спирмена
В ряде случаев, при относительно большом числе наблюдений, больших по вели чине показателях и значительном по объему исходном матери але, выполнение корреля ционного анализа при отсутствии средств вычислительной техники требует больших за трат времени. В этих случаях можно прибегнуть к анализу не самих показателей, а их ус ловных номеров (рангов). С этой целью применяется коэффициент корреляции рангов ( r ), предложенный Спирменом. Он показан также в тех случаях, когда необходимо устано вить связь показателя здоровья населения с факторами, которые можно измерить лишь полуколичественно. Легкий в вычислении, но недостаточно точный, он применяется в ориентировочных исследованиях при необходимости получения быстрого результата. Коэффициент корреляции рангов Спирмена относится к непараметрическим критериям, основан на определении ранга (места) каждой из вариант вариационного ряда. Схема расчетов коэффициента корреляции рангов представлена в таблице.....
Таблица .....
Схема расчета коэффициента корреляции рангов Спирмена
| Признак Х | Признак Y | Ранги | dХ'Y' | d 2 XY | ||
| X' | Y’ | |||||
| XI Х2 X3 ...... Хn | YI Y2 Y3 ..... Yn | X’1 Х'2 Х'3 ...... Х'n | У'1 У'2 У3 ...... Уn | dХ'1У'1 =X'1 - Y1 dХ'2У'2 dХ' 3У'3 ................. dХ'nУ'n | ||
| å dXY = 0 | åd2 X’Y’ |
Ход вычислений состоит из следующих операций. Сначала в обоих вариационных рядах производится ранжирование вариант (x и y) по их количественному значению. Для этого без изменения исходного местополо жения вариант в вариационных рядах каждой, в зависимости от ее величи ны, присваивается порядковый номер, начиная с единицы в естественном порядке чисел (x' == 1, 2, 3, ..., n и y' = 1, 2, 3, ..., n). При проведении этой процедуры важно соответствие ранжирования обоих вариационных рядов. Если первый ряд ранжировался, начиная от минимального значения к мак симальному, то и ранжи рование второго ряда должно также идти от мало го значения к большему. Если в вариа ционном ряду имеются варианты с одинаковыми значениями, то им присваивается ранг, равный среднему из суммы очередных порядковых номеров. Порядок действий при этом следующий: одинаковым по величине вариантам присваиваются смежные номера рангов в соответствии с их значением; производится расчет сред ней арифметической значений присвоенных рангов; первоначально присво енные ранговые номера заменяются на полу ченную срднюю величину. Далее попарно вычисляются величины отклонении значимос ти рангов первого ряда от второго ((dх'y'). Сумма отклонений должна быть равна нулю.
Полученные при проведении предыдущих операций отклонения возводятся в квадрат и квадраты отклонений суммируются. Наконец, производится расчет коэффициента кор реляции рангов по формуле:
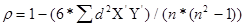 , где
, где
условные обозначения представлены в таблице.
Оценка достоверности коэффициента корреляции рангов производится сопос тавлением с критическими величинами по специальной таблице. Если полученное зна чение r меньше r0,05, то корреляция признается незначимой. Таблица используется при числе парных наблюдении от 5 до 40. Кроме того, может быть расчитана средней ошиб ки коэффициента корреля ции рангов. Для этого рассчитывают среднюю ошибку коэф фициента корреляции по формуле: mr = (1- rYX2 )/ Ön.
При малой выборке (n < 30) для этой цели используется формула:
mr = Ö((1- rYX2 )/n-2).
Величина коэффициента корреляции рангов считается достоверной, если она не менее чем в 3 раза превышает свою среднюю ошибку. В противопо ложном случае корреля ционная связь признается незначимой.
Среди методов определения степени связи между качественными признаками необходимо отметить коэффициент ассоциации (Q). Примером применения коэффициен та ассоциации являлся оценка количественных результатов иммунопрофилактики, часто при меняемая в эпидемиологической практике. Для его расчета необходимо располагать только абсолютными данными, распределенными в четырехклеточной таблице на 2 груп пы : привитые (опытную группу, в таблице численные значения «a» «b») и и не приви тые (контрольную групуу, в таблице - значения «c», «d») и сведениями о заболевших («a», «c») в каждой из них за наблюдаемый период, то есть альтернативными признака ми являются факт заболевания и его отсутствия.
Коэффициент ассоциации рассчитывается по формуле:
QYX = (ad - bc) / (ad + bc).
. Величина и знак коэффициента ассоциации оцениваются аналогично коэффициенту кор реляции. Коэффициент ассоциации дает достаточно точную оценку коэффициента корре ляции при значениях между ±1.0 и ±0.5. Ниже 0.5 он дает значительные расхождения с коэффициентом корреляции, поэтому в практике эпидемиологического анализа находит применение в меньшей степени.
Дата добавления: 2016-03-22; просмотров: 1146;
