Регрессионный анализ

Коэффициент корреляции, рассмотренный выше, предедставляет собой суммарн ую количественнуто характеристику тесноты связи одним числом для всей совокупности исследуемых признаков. При изучении формы корреляционной связи (прямолинейная или криволинейная) встает вопрос о нахождении линии, выражающей зависимосгь явле ния-следствия (y) от явления-причины (x). Тенденция взаимосвязанных изменений может быть нисходящей или восходящей. При графическом изображении тенденций получают ся прямые или кривые линии, характеризующие корреляционную связь. Эти линии назы ваются линиями регрессии. В случаях, когда линия регрессии представляется прямой, между изучаемыми явлениями существует прямая корреляционная связь, а тенденция изменения выражается уравнением Ут=а+bx. Если предполагаемая связь показателя здоровья с гипотетической причиной (фактором окружающей среды) имеет криволиней ный характер, то для ее описания и оценки используют уравнения нелинейной регрес сии. Подбор уравнения для описания изучаемой корреляци онной связи производится с использованием метода наименьших квадратов.

Регрессией называется соотношение числового изменения одной величины к чис ловому изменению другой. Степень изменения одной величины при соответствующем изменении другой принято оценивать по коэффициенту регрессии. Результаты регрес сионного анализа при изучении причинно-следственных связей позволяют судить о вели чине изменения изучаемою явления (показателя здоровья) в зависимости от величины изменения причинного фактора (фактор окружающей среды, профилактические меро приятия, условия жизни и т.д.).

Коэффициент прямолинейной регрессии явления-следствия (у) относительно яв ления-причины (х) определяется по формуле: b_YX = r _yx * (s_y/s_x), где

b_YX - коэффициент регрессии, r _yx - коэффициент корреляции, s_x - среднее квадратическое отклонение ряда характеристик изучаемого фактора окружающей среды, а s_y - среднее квдратическое отклонение вариационною ряда анализируемого показате ля заболеваемости (смертность и др.). Как указывалось выше, линия прямолинейной регрессии, характеризующая корреляционную связь, описывается уравнением Ут=а+bx. Для определения параметров уравнения «а» и «b» ( «b» -коэффициент регрессии) ис пользуются следующие рабочие формулы:

;

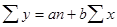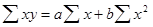
Совместное решение этих уравнений приводит к определению численных значе ний неизвестных параметров «a» и «b»:

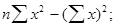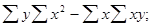D= A = B= 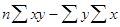, откуда

a = A/D и b=B/D

Регрессионный анализ является основой современных методов изучения много летней динамики, изложенных выше. Он широко применяется в интересах ретроспек тивного эпидемиологического анализа, прогнозирования заболеваемости и определения других показателей здоровья.