Основные типы задач и методы их решения. 1. Расчет сопротивлений, падений напряжения, токов утечки в сплошной проводящей среде.
а) Классификация
1. Расчет сопротивлений, падений напряжения, токов утечки в сплошной проводящей среде.
Метод решения. Непосредственное интегрирование выражения 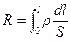 . Использование закона Ома в дифференциальной и интегральной форме.
. Использование закона Ома в дифференциальной и интегральной форме.
2. Расчет электрических цепей (нахождение токов, падений напряжений и т.д.).
Метод решения. Использование обобщенного закона Ома, правил Кирхгофа. При их использовании рекомендуется придерживаться следующего правила знаков: ток берется со знаком плюс, если его направление (заданное или предлагаемое) совпадает с выбранным направлением обхода контура или участка цепи; ЭДС источника берется со знаком плюс, если направление сторонних сил совпадает с выбранным направлением обхода.
3. Расчет работы, тепловой мощности, КПД источника тока.
Метод решения. Использование закона сохранения энергии, закона Джоуля-Ленца.
4. Переходные процессы в цепи с конденсатором (зарядка и разрядка конденсатора).
Метод решения. В процессах разрядки и зарядки конденсатора ток можно считать квазистационарным, т.к. его изменение происходит не слишком быстро. Квазистационарные токи можно описывать законами постоянного тока, если только их применять к мгновенным значениям величин.
б) Примеры решения задач
1. Цилиндрический воздушный конденсатор с внутренним (R1) и внешним (R2) радиусами заряжен до разности потенциалов 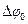 . Пространство между обкладками заполняют слабопроводящей средой с удельным сопротивлением ρ. Определить силу тока утечки, если высота конденсатора равна h.
. Пространство между обкладками заполняют слабопроводящей средой с удельным сопротивлением ρ. Определить силу тока утечки, если высота конденсатора равна h.
Решение.
В случае слабопроводящей среды изменением разности потенциалов 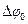 можно пренебречь, считая
можно пренебречь, считая 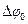 = соnst. Так как участок однородный, то
= соnst. Так как участок однородный, то
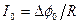 ,
,
где R – полное сопротивление участка.
Величину R определим путем интегрирования. Элементарное сопротивление тонкостенного цилиндрического слоя толщиной dr и радиусом r составляет
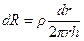 ,
,
откуда
 .
.
Следовательно,
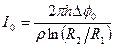 .
.
2. Определить сопротивление изоляции на один погонный метр длины провода диаметром d = 2 мм, если диаметр наружной проводящей оболочки равен D = 4 мм, а удельное сопротивление фарфоровой изоляции равно ρ=1013Ом·м.
Решение.
По закону Ома в дифференциальной форме
 .
.
Напряженность электрического поля Е выразим через потенциал
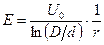 ,
,
где U0 – напряжение между проводом и наружной оболочкой изоляции.
С учетом получененного выражения
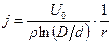 ,
,
а полный ток, отнесенный к длине провода l, будет
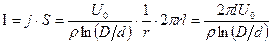 .
.
Таким образом, в соответствии с законом Ома сопротивление изоляции на единицу длины будет
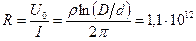 Ом.
Ом.
3. Определить силу тока, текущего через элемент ε2, если ε1 = 1 В, ε2 = 2 В, ε3 = 3 В, r2 = 1 Ом, r2 = 0,5 Ом, r3 = 1/3 Ом, R4 = 1 Ом, R5 = 1/3 Ом.
Решение.
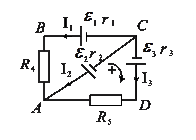 Для расчета цепи воспользуемся правилами Кирхгофа. Сначала выберем произвольно направление токов в ветвях так, как показано на рисунке. В соответствии с первым правилом Кирхгофа для узла А получим
Для расчета цепи воспользуемся правилами Кирхгофа. Сначала выберем произвольно направление токов в ветвях так, как показано на рисунке. В соответствии с первым правилом Кирхгофа для узла А получим
I1 +I2 +I3 = 0.
Для узла С первое правило Кирхгофа ничего нового не дает. Выберем теперь за положительное направление обхода замкнутых контуров направление по часовой стрелке. По второму правилу Кирхгофа для контуров АВСА и ACDA будем иметь
-ε1 +ε2 = -I1 (R4 +r1) + I2r2;
-ε2 +ε3 = I3 (r3 +R5) – I2r2.
Решая полученную систему уравнений, находим
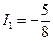 А,
А, 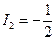 А,
А, 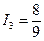 А.
А.
Знак “-” в значениях сил токов I1 и I2 показывает, что выбранное направление ошибочно. В действительности токи I1 и I2 текут в обратном направлении.
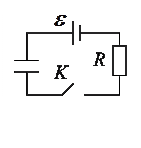 4. К источнику с электродвижущей силой ε подключены последовательно конденсатор емкостью С и резистор R. Найти закон изменения со временем заряда на обкладках конденсатора. Определить работу, совершаемую источником при заряде конденсатора, и количество теплоты, выделяющейся при этом в цепи.
4. К источнику с электродвижущей силой ε подключены последовательно конденсатор емкостью С и резистор R. Найти закон изменения со временем заряда на обкладках конденсатора. Определить работу, совершаемую источником при заряде конденсатора, и количество теплоты, выделяющейся при этом в цепи.
Решение.
На основании обобщенного закона Ома получим
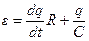 .
.
После разделения переменных уравнение примет вид
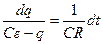 .
.
Интегрируя данное выражение в пределах от 0 до t и от 0 до q, после потенцирования получим закон изменения со временем заряда на обкладках конденсатора
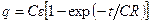 .
.
Работа, совершаемая источником за все время зарядки конденсатора,
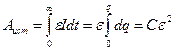 ,
,
где qк = Сε – конечный заряд конденсатора.
Количество теплоты, выделившейся за все время зарядки на сопротивление R, может быть найдено из закона сохранения энергии
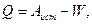
где 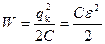 - энергия заряженного конденсатора.
- энергия заряженного конденсатора.
С учетом найденного значения Аист получим
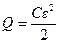 .
.
Это выражение может быть получено и независимым путем из закона Джоуля-Ленца:
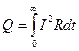 ;
;
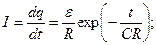
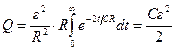 .
.
Дата добавления: 2016-03-22; просмотров: 1719;
